摘  要： 通过构建超声回波信号模型，将基于小波包阈值去噪应用在超声回波信号研究中。针对超声回波信号的非平稳性，提出一种多阈值分段去噪方法应用于超声回波信号的去噪研究中。仿真实验表明，采用的多阈值分段去噪克服了单阈值规则的局限性，能够较好地处理超声信号中的噪声分量。

　　关键词： 超声回波信号；小波包阈值去噪；非平稳性；多阈值

0 引言

　　超声无损检测技术是通过换能器发射脉冲与被检测对象相互作用，并接收目标的反向散射回波来进行相关研究，达到对检测对象进行宏观缺陷、几何特性、组织结构和力学性能等特定性评价的非侵入式检测技术[1]。超声检测的回波信号是时频有限的非平稳信号，需要表示局部时间范围内的频谱信息，传统的频域或时域分析方法不能满足回波信号处理的要求。而小波变化由于具有灵活性、快速性、时频双域性等特点，成为分析非平稳信号的一种重要工具[2]。

　　小波去噪是小波变换在信号处理中的关键应用之一，主要方法有模极大值去噪、相关性去噪、小波阈值去噪等，其中小波阈值去噪因计算量较小，能保持信号奇异性被广泛应用[3]。小波包阈值去噪在对信号低频部分进行分解的同时，还能对信号的高频部分进行分解，有效地提取各频段的有用信息，更适合高精度的超声回波信号分析[4]。目前传统的几种单阈值规则去噪方法因各自的局限性，无法在噪声污染不稳定的各个频段实现高精度去噪。为此提出一种多阈值分段去噪的方法，它克服了单阈值规则的局限性，仿真实验结果也表明了这种去噪方法的可行性和优越性。

1 超声传播特性及回波信号模型

　　超声检测声源一般由若干探头晶片组成，发射的声波形成一个沿着有限范围向一定方向传播的超声束。超声波在介质中传播，并接收目标的反向散射回波，通过对获得的目标回波进行分析，确定反射目标的物理特性和传输路径上的各种信息。然而超声波在传播过程中由于受到声束散射、介质吸收、异质界面的弹性反射以及外界加性噪声的影响，所接收的回波信号会发生一些噪声污染，因此精确的回波信号至关重要。经研究发现，超声回波存在非线性现象，这种现象可用模型逼近。常用的超声脉冲经验模型有高斯脉冲模型、混合指数模型和双指数模型，其参数设置灵活、估计精度高，被广泛应用于模拟仿真中。

　　超声换能器的脉冲响应可模拟成高斯信号，响应的脉冲幅度可表示为：

　　而底面回波、缺陷回波与材料散射波信号的产生机理十分相近，都是发射的超声波入射到试件中遇到阻碍时，产生的波反射和散射信号。在宽带窄脉冲超声检测中，根据超声回波的物理特性，忽略在实际检测中缺陷反射对超声脉冲频率的影响，用超声换能器脉冲响应幅度的修改模型s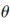（，t）表示接收到的有用回波信号[5]：

　　回波模型做加性噪声处理可得含噪超声回波模型：

　　x（t）=s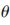（，t）+v（t）（3）

　　其中，v（t）为加性高斯噪声。

2 小波包理论

　　小波分析是将任意信号f（t）表示为小波函数的线性组合，Mallat[6]在多分辨率分析的基础上提出正交小波变换分解与重构的快速算法：信号f（t）的j层小波分解是将f（t）以尺度j变换到空间L2（R）的两个正交子空间Vj和Wj上，由Vj得到离散逼近值cAj，由Wj得到离散细节值cDj，下层分解中以尺度j+1再将cAj分解到子空间Vj+1和Wj+1中，这样不断分解下去，实现对信号的多分辨率分解。

　　设{hn}n∈Z是正交尺度函数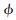（t）对应的正交低通实系数滤波器，{gn}n∈Z是正交小波函数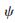（t）对应的高通滤波器，其中gn=（-1）nh1-n，则它们满足以下两尺度方程和小波方程：

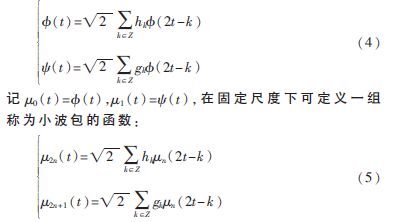
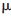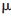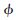　　递归定义的函数n（n=0，1，2...）称为由正交尺度函数0=确定的小波包。

3 小波包阈值去噪

　　3.1 小波阈值

　　超声回波信号中所含噪声大多为高斯噪声，噪声对应的小波系数分布相近、个数多、幅值小。而回波信号经小波变换后可认为由信号产生的小波系数包含信号的重要信息，其幅值较大，数目较少。据此，设置一个合适的阈值，大于该阈值的小波系数判定为有用信号，予以保留；小于该阈值的小波系数判定为噪声，予以剔除。最后将处理后的小波系数利用逆小波变换进行重构，恢复有效信号，达到去噪目的[7]。

　　小波变换由于分析窗的面积是固定的，高的时间分辨率对应差的频率分辨率，针对超声回波信号包含一定中、高频率的时变信号这一特性，不能提供很好的频率分析。小波包变换在多分辨率分析的基础上对小波空间做了更精细的分割，特别是对高频部分进一步分解。在小波包分解中，每一个高频系数向量也像低频部分一样分解成为两个部分，这种方法提供了更加丰富的分析方法，达到细致的刻画效果，提高了超声检测信号的分析能力。

　　3.2 小波包分解与重构

　　3.3 小波包阈值规则

　　N为噪声信号经小波分解得到的小波系数总和，?滓为噪声信号均方差，阈值选择规则[9]如下。

　　（1）Sqtwolog规则：采用Donoho和Johnstone统一阈值：

　　（2）Rigrsure规则：采用基于Stein无偏似然估计原理的自适应阈值。设p=[p1，p2，…，pN]，且p1≤p2≤…≤pn，p的元素为小波包系数的平方，按由小到大的顺序排列。设R为风险向量，其元素为：

　　三种阈值规则各有特点，Sqtwolog阈值规则是将全部系数进行处理，因此去噪效果较强，但容易过度去噪，称为“激进”规则，适合高频部位；Rigruse阈值规则以及Minimaxi阈值规则是将部分系数进行处理，是较为保守的处理方法，可防止过度去噪，但也容易出现去噪不足，称为“温和”准则，适合低频部分。

　　3.4 多阈值分段去噪

　　噪声在频率域上的分布主要集中在频率较高的部分，在利用小波包去噪时，假如不同频段信息采用同种阈值处理方法，或同一个频段信息采用不同阈值处理方法都会影响去噪精度[10]。

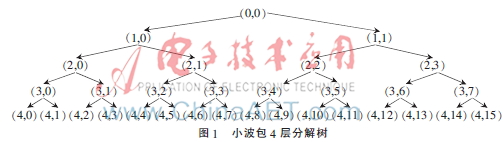
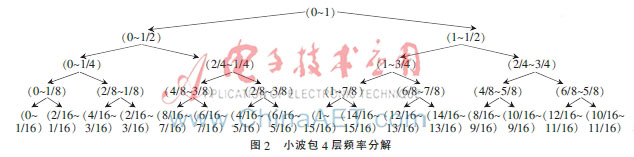
　　由图1、图2可以发现，小波包树节点的自然顺序与频率顺序存在不一致的现象。最低频部分对应的是第一个节点，最高频部分对应的是第九个节点。因此可以将一种多阈值分段去噪的方法应用于超声信号检测中。具体做法是：取低频节点（4，0）为A段，高频节点（4，8）为C段，剩余节点分在中频段为B段，在A段采用Rigruse阈值规则，在B段采用Minimaxi阈值规则，在C段采用Sqtwolog阈值规则。

4 仿真实验

　　基于式（2），取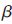0.4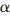，=25（MHz）2，fc=5 MHz，τ= 3.5 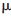s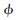，=1.8 rad，构建超声回波信号。基于式（3），添加随机高斯色噪声，得到模拟含噪超声回波信号。针对加噪后的信号，分别采用Sqtwolog阈值规则、Rigruse阈值规则、Minimaxi阈值规则和上文提到的多阈值分段规则进行去噪比较。其他条件统一为：采用sym4小波基，分解层数4层，软阈值处理。仿真结果如图3所示。

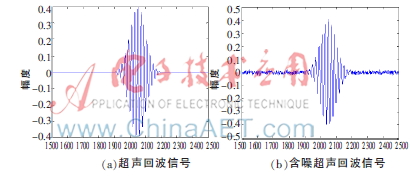
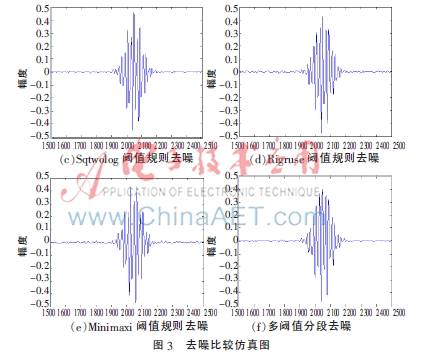
　　如图3所示，（c）图中采用Sqtwolog阈值规则，相比（b）图含噪信号，有良好的去噪效果。但相比（a）图原始信号，有用信号失真较为严重，属“激进”去噪；（d）图和（e）图分别采用Rigruse阈值规则和Minimaxi阈值规则去噪，信号失真较小，但去噪效果不及Sqtwolog阈值规则，属“温和”去噪；从（f）图中可看出，基于多阈值分段去噪的方法有用信号保留相对完整，整体去噪效果相对平滑。

　　为了更精确地区分这四种去噪方法的效果，将20组随机高斯色噪声加入超声回波信号中，去噪处理前平均信噪比为15.910 7。选用信噪比（SNR）、均方根误差（RMSE）、与原始信号的互相关系数（ρ）、平滑度（?酌）作为评价小波包阈值去噪对信号的处理效果[11-12]。信噪比为有用信号的能量与噪声能量之比，信噪比越大越好；均方根误差指重构后信号与原始信号的均方根误差，其值越小表示去噪效果越好；互相关系数为原始信号与重构信号的方差，其值越接近1越好；平滑度是反映重构信号的平滑程度，平滑度越小则信号处理效果越好。比较结果如表1所示。

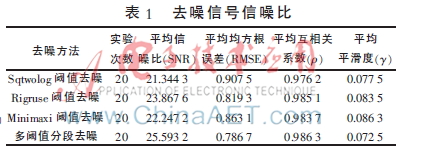
　　如表1所示，从信噪比和均方根误差分析来看，在单阈值去噪方法中，Rigruse阈值规则去噪效果最明显。但采取多阈值分段的方法进行去噪，比全局单阈值的方法要好。因为Sqtwolog阈值规则去噪更适合高频去噪，而超声回波信号的大部分有用信息在低频部分，所以平均信噪比最差。Rigruse阈值规则去噪和Minimaxi阈值规则去噪在中低频部分去噪效果良好，在超声回波信号处理中优于Sqtwolog阈值规则去噪。多阈值分段去噪在高频段采用了Sqtwolog规则，使其在有用信息含量较少的部分采用“激进”去噪，在有用信号大量集中的低频段采用单阈值去噪效果最好的Rigruse规则，在中频段采用相对“温和”的Minimaxi规则，所以去噪效果最好；从互相关系数的数据分析中可以发现，采取Sqtwolog阈值规则其信号失真较严重，而多阈值分段去噪和Rigruse规则都对有用信号保留比较完整；从平滑度来看，Sqtwolog阈值规则去噪后较平滑，而Rigruse阈值规则是直接将一部分的高频系数置0，虽很好地保留了信号的真实成分，但去噪后平滑度较差。从数据中可以看出，采用的多阈值分段规则进一步完善了Sqtwolog规则的信号处理效果，去噪后数据更加平滑，局部突变较小，更接近原始信号。

　　整体来说，四种不同的方法都能达到一定的去噪效果。但不同的阈值规则选取对最终去噪效果影响很大。本文通过分析单阈值规则去噪的各自优劣，结合Sqtwolog、Rigruse、Minimaxi这三种不同单阈值规则的表现而改进的多阈值分段去噪方法，使信噪比得到显著提升，很好地保留了有用信号，整体去噪效果更平滑，特别适用于有用信息丰富的超声回波信号处理。

5 结束语

　　本文通过将小波包分解按照频率重新排列为高、中、低三个频段，在不同频段采用更加适合的阈值规则，进而将多阈值分段去噪应用在对超声回波加噪信号的处理上。通过实验仿真比较表明，多阈值分段去噪在超声回波信号去噪中效果明显，并最大程度地保留了有用信息，减少了信号失真，为解决实际超声回波含噪信号的去噪问题提供了一种有效的信号处理方法。

　　参考文献

　　[1] 罗雄彪，陈铁群.超声无损检测的发展趋势[J].无损检测，2005，27（3）：148-152.

　　[2] 崔治.小波分析在超声检测信号处理中的应用研究[D].长沙：湖南大学，2012.

　　[3] 郭建峰.图像小波阈值去噪方法研究[J].电脑知识与技术，2014（22）：5291-5292，5300.

　　[4] 郑建国，石智，权豫西.非平稳信号的小波包阈值去噪方法[J].信息技术，2007，31（3）：16-18，55.

　　[5] 卢振坤.参数化的超声回波模型及其参数估计[D].广州：华南理工大学，2013.

　　[6] MALLAT S. Theory for multi-resolution signal decomposition： the wavelet represention[J]. IEEE Transactions on  Pattern Analysis and Machine Intelligence， 1989，11（7）：674-693.

　　[7] 张燕.超声缺陷回波信号小波阈值去噪方法研究[D].南京：南京邮电大学，2012.

　　[8] 孙延奎.小波分析及其应用[M].北京：机械工业出版社，2005.

　　[9] 陈晓曦，王延杰，刘恋.小波阈值去噪法的深入研究[J].激光与红外，2012，42（1）：105-110.

　　[10] 章浙涛，朱建军，匡翠林，等.小波包多阈值去噪法及其在形变分析中的应用[J].测绘学报，2014，43（1）：13-20.

　　[11] 陶珂，朱建军.多指标融合的小波去噪最佳分解尺度选择方法[J].测绘学报，2012，41（5）：749-755.

　　[12] 李宗春，邓勇，张冠宇，等.变形测量异常数据处理中小波变换最佳级数的确定[J].武汉大学学报（信息科学版），2011（3）：285-288.