于路，薄华

　　（上海海事大学 信息工程学院，上海 201306）

　　摘要：针对现有的单一特征提取算法对运动想象脑电信号识别率不高的问题，提出一种以相关系数改进的经验模态分解（EMD）的特征提取算法。对已有的BCI竞赛数据中C3、C4两个通道脑电数据进行预处理，之后通过EMD对脑电信号进行分解，得到IMF分量。通过计算原始信号与各阶IMF分量之间的相关系数，选择具有较大相关系数的IMF作为特征，由这些IMF分量的能量特征和平均幅值差来组成脑电信号的特征。使用支撑矢量机分类器（SVM）对左右手运动想象脑电信号进行分类。实验结果表明，基于相关系数改进的EMD脑电信号的处理方法明显优于只用EMD的脑电处理方法，得到的最高正确识别率为88.57%。从而证明了该方法的有效性。

　　关键词： 脑电信号；经验模态分解；相关系数；特征提取

0引言

　　头皮脑电（Electroenc EphaloGraph,EEG）信号是一种产生机理相当复杂且非常微弱的随机信号，它反映了大脑阻止的脑电活动及大脑的功能状态。不同的思维状态在大脑皮层有不同的反映［1］。

　　脑机接口（BrainComputer Interface，BCI）不依赖于大脑外周神经与肌肉系统，是大脑与计算机或其他电子设备之间建立可直接交流和控制的通道，可以有效增强身体严重残疾的患者与外界交流或控制外部环境的能力，提高患者的生活质量，同时也在娱乐电竞等领域有着巨大的应用前景［2-5］。

　　目前EEG特征提取的常用方法有FFT、SFT、AR［5］、AAR［6］、ICA、小波分析［7］、特定频带的功率谱等方法。经典的FFT在分析确定信号和平稳信号时发挥了重要作用,但利用FFT分析突变信号的频谱存在局限性。SFT在一定程度上克服了标准FFT不具有局部分析能力的缺陷,在某些信号处理中发挥了一定的作用，但也存在不可克服的缺陷。SFT是时间窗内信号特征的平均,时间窗内信号越短,获得的时间分辨率就越高。根据信号测不准原理,时间局域化性质和频率局域化性质是矛盾的。AAR模型参数随每一样本点的输入而改变,因而更好地反映了大脑的状态。但是，该方法更适合分析平稳信号，对包含高度非平稳信号的运动想象EEG，该模型达不到理想效果。小波变换和小波包变换分解信号时，要预先设好分层数和小波函数，不具备对信号自适应的分解能力。因此需要采用一种非线性分析的方法，该方法同时具有对信号自适应的分解能力，能通过度量脑电信号的复杂度来反映脑电的特征。本文中采用的是用相关系数改进经验模态分解的脑电信号处理方法，可以获得一系列固有模态函数分量（Intrinsic Mode Function，IMF）。将这种方法应用到脑电信号的处理过程中能得到较好的效果。

1EMD算法

　　经验模式分解算法(Empirical Mode Decomposition,EMD)［8］是一种自适应的数据处理或挖掘方法，非常适合非线性非平稳的时间序列。其本质是通过数据的时间尺度来获得本征波动模式，然后分解数据。这种分解过程可以形象地称之为“筛选（sifting）”过程。

　　在理论上，EMD可以应用于任何类型的时间序列（信号）的分解，因而在处理非平稳及非线性数据上，比之前的方法具有更明显的优势。所以，EMD［9-10］方法一经提出就在不同的工程领域得到了迅速有效的应用。

　　该方法的关键是它能使复杂信号分解为有限个本征模函数，所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征信号。EMD分解方法基于以下假设条件：

　　(1)数据至少有两个极值，一个最大值和一个最小值；

　　(2)数据的局部时域特性是由极值点间的时间尺度来唯一确定；

　　(3)如果数据没有极值点但有拐点，则可以通过对数据微分一次或多次求得极值，然后再通过积分来获得分解结果。

　　设原始信号为X(t),EMD算法的计算步骤如下：

　　（1）找出原数据序列X(t)的所有极大值点和极小值点，将其用三次样条函数拟合为原序列的上、下包络线,分别为u(t)和v(t)，可得包络线的平均值m11：

　　m11=1/2(u(t)+v(t))(1)

　　（2）将原数据序列减去包络平均值m11，得到一个减去低频的新序列h11:

　　h11=X(t)－m11(t)(2)

　　（3）h11不一定是平稳数据序列，用h11(t)代替原始信号X(t),重复上述过程k次,直到所得包络趋近于零，这样可以得到第一个本征模函数（IMF）。分量c1=h1k(t)，它表示信号数据序列最高频率的成分。

　　（4）用X(t)减去c1，得到一个去掉高频成分的新数据序列r1；对r1再进行上述分解，得到第二个本征模函数（IMF）分量c2；如此重复:

　　r2=r1－c2

　　r3=r2－c3

　　…

　　rn=rn－1－cn

　　（5）当第n个剩余量rn已成为单调函数，无法再分解IMF时，整个EMD分解过程完成。原始信号可以表示为将一个频率不规则的波化为多个单一频率的波与残波相加的形式。即：

　　X(t)=∑ci+rn(3)

　　然而脑电信号其背景噪声很强，在对脑电信号进行EMD分解时，通常不能将信号与噪声彻底分开，在每一个输出的轨道之中，或多或少都掺杂着一些噪声，选择合适的IMF分量显得尤为重要。这里引入相关系数的概念，借此权衡各个IMF的有效性。

2运动想象脑电信号识别算法

　　2.1基于相关系数的特征提取

　　相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法进行计算，同样以两变量与各自平均值的离差为基础，通过两个离差相乘来反映两变量之间的相关程度。是判断特征选取的一个方法。

　　相关系数的定义：假设有两个随机变量X和Y，则它们的相关系数为：

　　r=Cov(X,Y)σXσY

　　=E［{X－E(X)}{Y－E(Y)}］［E{X－E(X)2}］12［E{Y－E(Y)}2］12(4）

　　其中，Cov(X,Y)为随机变量X与Y的协方差函数，σX、σY分别指X、Y的标准差，E(X)、E(Y)为两者的平均值。相关系数r的取值范围是［-1,1］，表示变量之间相关程度的高低，r的绝对值越大，说明这两个变量之间相关程度越高。r>0表示正相关，r<0表示负相关，特殊地，r=1称为完全正相关，r=-1称为完全负相关，r=0称为不相关。

　　对原信号进行EMD分解后，得到n阶IMF分量和残波。根据各个IMF分量与原信号的相关系数来选择更合适的IMF分量。设原信号序列为X(n),信号的IMF分量为Yi(n),其中i表示第i个IMF分量，则相关系数的定义如下：

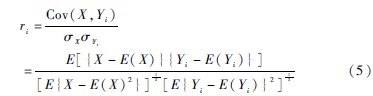
　　使用EMD分解原信号得到IMF分量后，在众多分量中包含的有用信息各不相同，同时包含了噪声。为了得到更好的特征，提高左右脑电信号的分辨率，本文通过相关系数选择合适的分量。分别取各阶IMF分量的能量单独作为该信号的特征，因为每组脑电信号只取一个IMF分量，所以这里只考虑能量特征。计算公式如下：

　　El=∑ni=1［c(i)2］(6)

　　其中，El对应了第l个IMF分量的能量，c(i)表示该分量中的第i个数值，n表示该分量的长度。本文中n为140。

　　一组信号可得到唯一能量特征。表1给出各阶IMF分量与原信号之间的相关系数，及只取相应能量特征作为脑电信号的特征后的左右手脑电信号识别率。

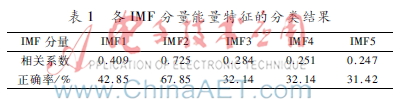
　　由表1可知，IMF2分量与原信号的相关系数最大，最适合进行特征提取。各阶IMF分量以与原信号的相关系数从大到小排列，分别为IMF2、IMF1、IMF3、IMF4和IMF5。当IMF分量与原信号的相关系数越大时，采用该分量作为条件提取特征得到的信号识别率越高，从而该IMF分量比其他IMF分量更适合进行特征提取。

　　然而只用单一的IMF分量并不能达到很高的识别率。这里考虑使用多个IMF分量进行特征选取。当选取多个IMF分量时，除能量特征外，脑电信号的特征还包括平均幅度差。

　　在进行EMD算法分解时，得到的各阶IMF分量是从高频到低频的脑电信号分解，所以可以看出，同阶不同通道信号之间有时幅值波动相差过大，因此此处定义平均幅度差作为一个特征值，计算公式如下：

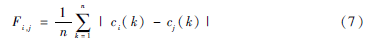
　　其中，ci是第i个IMF分量，cj表示第j个分量(i≠j),n为信号的长度，这里n为140。分别计算不同IMF分量个数来提取特征时的脑电信号分类正确率，如表2所示。

　　表2中，分量顺序根据与原信号的相关系数从大到小排列，分别是：IMF2、IMF1、IMF3、IMF4、IMF5。分量选取从第一个开始取，如当IMF分量个数为2时，所取分量为IMF2、IMF1。实验数据表明，取前3个分量达到了最好的分类效果。当所取IMF分量个数过多时，信号包含的无效信息比例也会同时增加，对分类会造成更大的影响，且前3个分量包含了原始信号约90%的能量，故能达到较好效果。

　　2.2本文算法

　　本文选择的脑电信号识别算法是基于相关系数改进的EMD算法。EMD算法是一种非线性分析方法，同时具有对信号自适应的分解能力，能通过度量脑电信号的复杂度来反映脑电的特征。对得到的脑电数据进行预处理后，进行EMD分解从而得到IMF分量和余量。但是脑电信号中仍然包含了无用信息，在使用EMD算法进行分解过程中，无法将噪声信号彻底分解出来。故采用基于相关系数改进的EMD算法，选择与原信号相关系数最大的3个IMF分量：IMF1、IMF2、IMF3。由这3个分量可以得到3个能量特征和两个平均幅度差特征，送入SVM［1112］进行分类。在SVM过程中先用训练数据得出训练模型，再用测试数据得到实验结果。本文算法的具体步骤如下：

　　（1）对脑电信号进行预处理；

　　（2）从训练数据中取一组信号中1 s的脑电数据进行EMD算法分解；

　　（3）计算各阶IMF分量与原信号的相关系数，选出3个相关系数最大的IMF分量；

　　（4）由IMF分量得到能量特征和平均幅度差；

　　（5）将数据特征送入SVM进行训练；

　　（6）载入测试数据得到结果，从而得出实验结论。

3实验分析

　　3.1实验数据

　　本文实验数据采用奥地利格拉兹工业大学脑机接口研究中心提供的运动想象脑电数据(Data setⅢ)［13］。该数据集的受试主体为25岁女性，主体以放松状态坐在显示器前，显示器呈现提示信息。根据出现的左右线索想象左右手运动，从而得到反馈数据，其中左右线索的顺序是随机的。

　　实验共得到280次长度为9 s的脑电数据，140次为训练样本（70 次想象左手运动,70 次想象右手运动)，另140次作为测试样本。在前2 s主体保持放松，在第2 s屏幕出现十字光标，持续时间1 s，提示实验即将开始。第3 s 屏幕出现左右箭头，主体根据提示信息想象左右手运动，即该数据的有效时间段为4 s~9 s。

　　该信号的采集频率为128 Hz,再经过0.5~30 Hz的带通滤波器。实验采用Ag/AgCl电极，通过C3、Cz、C4三个通道获得反馈数据，其中，C3、C4电极位于大脑的初级感觉皮层运动功能区，能反映主体在想象左右手运动时大脑状态的变化，Cz作为参考电极。实际分析时只采用了 C3、C4 这 2 个通道的数据。

　　3.2实验分析

　　实验数据为280组长度为9 s的脑电数据，其中4~9 s为有效时间区间，但是考虑信号的有效性，选择4~8 s的脑电数据作为实验数据。以一个通道的1 s数据作为一小段数据进行EMD分解，得到IMF分量后，计算各阶IMF分量与原始信号的相关系数，按照相关系数由大到小选取最大的3阶IMF分量进行特征提取。对于一组一个通道中1 s的数据包含3个能量特征和2个平均幅值差，则一组数据一共包含40个特征。采用十折交叉验证法将训练数据的特征采样送入SVM，并确定SVM的核参数。将测试数据提取特征后送入SVM的分类模型进行分类。分类结果如表3所示。

　　从表3可以看出，采用结合相关系数的EMD特征提取方式能获得更高的识别率。其中训练集的识别率达到92.86%，测试集的分类正确率达到88.57%，这个结果非常接近BCI大赛中第一名的分类结果。由此改进后的EMD算法更加适合脑电特征提取。

　　4结束语

　　本文提出通过相关系数来改进EMD对脑电信号特征的提取［14］。通过分析EMD分量与原信号之间的相关系数来确定相应的特征组成特征向量，输入SVM分类器中，从而实现左右手运动想象脑电信号的分类。研究结果表明，采用相关系数改进的EMD提取脑电特征的正确率明显高于仅采用EMD的脑电特征提取方法。因此，基于相关系数改进的EMD算法在运动想象脑电信号的识别研究中具有很高的应用价值。

　　参考文献

　　［1］ 徐宝国，何乐生，宋爱国.基于脑电信号的人机交互实验平台的设计和应用［J］.电子测量与仪器学报，2008, 22(1):8185.

　　［2］ 高上凯. 浅谈脑机接口的发展现状与挑战［J］. 中国生物医学工程学报, 2007. 26(6):801803.

　　［3］ 王斐，张育中,宁廷会，等.脑—机接口研究进展［J］．智能系统学报，2011，6(3):189199．

　　［4］ TANAKA K,MATSUNAGA K,WANG H.Electroencephalogrambased control of an electric wheelchair［J］.IEEE Transactions on Robotics，2005，21( 4) : 762766．

　　［5］ 张毅，杨柳，李敏，等.基于AR 和SVM的运动想象脑电信号识别［J］．华中科技大学学报（自然科学版），2011，39(Z2):103106．

　　［6］ 徐宝国，宋爱国.单次运动想象脑电的特征提取和分类［J］．东南大学学报（自然科学版），2007，37(4):629633．

　　［7］ 李明爱，王蕊，郝冬梅．想象左右手运动的脑电特征提取及分类研究［J］．中国生物医学工程学报，2009，28(2):166170．

　　［8］ 张小莉，张歆，孙进才.基于经验模态分解的目标特征提取与选择［J］.西北工业大学学报，2006,24(4):453456.

　　［9］ 余炜，韩强，马晶晶，等.基于EMD和SVM的脑电信号处理方法［J］.昆明理工大学学报（自然科学版），2012,37(6):3842.

　　［10］ 金晶，王行愚，张秀，等.基于能量特征的左右手运动想象闹心好的识别方法［J］.科学通报，2001,46(3):257263.

　　［11］ 安文娟. Fisher和支持向量综合分类器［D］. 大连：辽宁师范大学, 2010.

　　［12］ 李金华.基于SVM的多类文本分类研究［D］. 青岛：山东科技大学,2010.

　　［13］ Sun Shiliang, Zhang Changshui.Adaptive feature extraction for EEG signal classification［J］. Medical & Biological Engineering & Computing,2006,44(10)：931935.

　　［14］ RAKOTOMAMONJY A, GUIGUE V. BCI competition III: dataset IIensemble of SVERP for BCI P300 speller［J］.IEEE Transactions on Biomedical Engineering, 2008, 55 (3):11471154 .