文献标识码: A
DOI:10.16157/j.issn.0258-7998.2016.07.003
中文引用格式: 何天光,杜江. 一种高性能低复杂度Polar Code编解码算法研究[J].电子技术应用,2016,42(7):13-16,25.
英文引用格式: He Tianguang,Du Jiang. An efficient and low-complexity encoding and decoding algorithm of Polar Code[J].Application of Electronic Technique,2016,42(7):13-16,25.
0 引言
在无线通信系统中,信道编码的目的是使信息在有噪声干扰的信道中能够可靠地传输。根据香农信息论[1]可知,任何通信信道的容量都有一个确定值C,如果通信系统中的传输速率R在满足条件R<C时,则存在一种信道编码,在不牺牲传输速率的情况下使信息码元的误码率趋于任意小。为此,许多信道编码领域的研究学者为达到这一目标做出了许多贡献。2009年,Arikan等人提出了极化码(Polar Codes)[2-5],是首次被严格证明能够达到香农极限容量的一种信道编码,而且编译码复杂度在随着码长增加时只保持对数增加。对于译码,连续抵消(Successive Cancelation,SC)译码[2,6]算法是Arikan针对极化码编码结构提出的译码方案。但是,SC译码算法在码长有限时的性能与Turbo码和LDPC码相比不能体现其优越性。因此许多学者在SC译码算法的基础上进行改进,并提出了许多高性能的译码方案。这些算法的性能经证明已经优于Turbo码和LDPC码[7-9],比如序列列表SC译码(List SC,SCL)[8-9]、堆栈SC译码(Stack SC,SSC)[10]、循环冗余校验码辅助SCL译码(CRC-SCL)[11]等算法。随着全球5G通信系统研究的展开,Polar Code也得到了学术界和国内外5G标准化研发机构的强烈关注。
1 Polar Code编码
1.1 编码原理
极化码(Polar Codes)是一种结构性与迭代性极强的信道编码,而且能够被严格证明它的渐进性能够达到香农极限容量。拥有如此高性能的信道编码是因为它的编码核心思想:基于信道极化现象,使其信道性能(可靠性)极好的信道传输有用信息,反之传输双方约定的固定信息。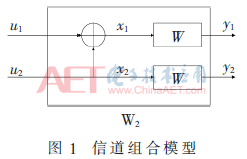
1.2 信道极化
对于任意N=2n(n≥0)个独立的二进制对称输入离散无记忆信道(B-DMC)进行递推方式组合[5],然后使其分裂后各个子信道的信道容量趋于两极化,随着码长N的增大,这些子信道的信道容量趋于两极化的程度愈加明显。因此这样的操作可称之为信道极化[2]。
例如当n=1时,两个独立的B-DMC信道W通过如图1所描述的方式组合成一个信道W2,这个过程可解释为:信道的输入信息为u1,u2∈{0,1},通过编码后为x1,x2∈{0,1}分别送入两个子信道,输出信号为y1,y2。
由此,可以通过信道转移概率W(y|x)来表示B-DMC信道的信道容量:

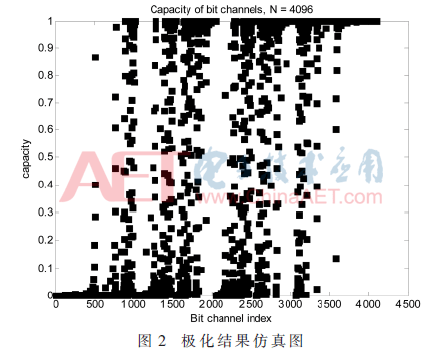
通过式(2)、(3)和(4)可知,两个子信道的信道容量一个较好一个较差,若N越大,极化效果会更加明显。通过信道的极化结果,可以挑选出性能好的信道传输信息,可称之为信息位;性能差的信道传输固定信息,可叫作固定位。
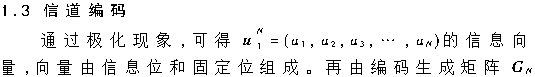

2 Polar Code译码
2.1 SC译码算法

为了计算公式更加简化和硬件可实现性,采用对数域的似然比(LLR)表示。由似然比进行译码判决:
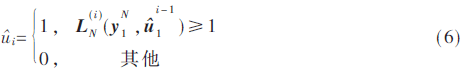
2.1.1 LLR(Log-Likelihood Ratio,LLR)计算方式
由于SC译码算法是Arikan针对极化码编码特性而设计出来的,那么它的译码结构和它的编码结构一样具有极其强的规则性。算法结构图如图3所示。

图中yi表示信道接收端接收的信号;![]() 表示接收的信号yi通过译码器译码后的输出值;λ表示层(Layer),图中每一列定义为一层:最左边λ=3(λmax=log2 N+1)定义为决策层,最右边λ=1为信道层,其他层统称为中间层;
表示接收的信号yi通过译码器译码后的输出值;λ表示层(Layer),图中每一列定义为一层:最左边λ=3(λmax=log2 N+1)定义为决策层,最右边λ=1为信道层,其他层统称为中间层;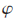 表示相位(Phase),就是译码器在每一层计算节点的LLR值的顺序,比如在本例中决策层的节点LLR值计算顺序应为图中节点的(1,3,2,4)。
表示相位(Phase),就是译码器在每一层计算节点的LLR值的顺序,比如在本例中决策层的节点LLR值计算顺序应为图中节点的(1,3,2,4)。
译码首先从决策层的节点1开始激活,来计算第一个码子的LLR值,以此判决出它的译码结果,但是计算此处的LLR值需要右边下一层节点5、7的LLR值。若这两个节点的值已知,那么通过计算即可得到节点1的LLR值,否者还需要再下一层(本例中的信道层)的9、10、11、12节点的LLR值来决定5、7节点的LLR值,最终算出节点1的LLR值。信道层的LLR值的计算公式: 在计算出节点1的LLR值之后,5、7节点的LLR值已知,根据蝶形图结构,可以直接算出第二个译码码子
在计算出节点1的LLR值之后,5、7节点的LLR值已知,根据蝶形图结构,可以直接算出第二个译码码子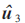 对应的节点3的LLR值。以此操作,直到计算出所有节点的LLR值为止。
对应的节点3的LLR值。以此操作,直到计算出所有节点的LLR值为止。
在译码过程中,当计算出某一个决策层节点的LLR值之后,首先需要判断当前节点对应的码元是否为信息位,如果是则根据式(6)可判决出当前码子的译码结果,否者该码子直接判决为0。
以上的描述是SC译码算法的LLR值计算方式和判决流程,下面将要讨论每一层(λ>1)各个节点的LLR值的计算公式。通过对译码结构分析可知在每一层中第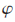 个节点的LLR值计算时的计算公式为:
个节点的LLR值计算时的计算公式为: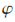 奇数时利用F函数进行计算,?渍为偶数时使用G函数。
奇数时利用F函数进行计算,?渍为偶数时使用G函数。



2.1.2 LLR存储结构
在进行决策层节点的LLR值计算时会产生对应中间层节点的LLR值和部分和数据,这些数据都是判决一个码子的重要依据。通过上一小节描述的译码计算方式中可知信道层和中间层的LLR值和部分和都需要存储。在LLR存储时,根据LLR计算特性,以层λ为单元进行存储,第λ层需存储的数据个数为n=2m-λ,m=log2 N+1。因此存储结构如图4。

根据部分和的计算规则可知,它的存储结构与LLR值的存储结构类似。根据SC译码算法的结构和硬判决特点,可知SC译码算法的空间复杂度和时间复杂度分别为O(N)和O(NlogN)。
通过以上对SC译码算法的研究不难发现,算法的一个潜在缺点是:判决当前码子![]() 的值时需要
的值时需要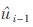 的参与,那么当前码子的判决结果会影响后续码子的判决值。
的参与,那么当前码子的判决结果会影响后续码子的判决值。
2.2 SCL(SC List)译码算法
根据SC译码算法的缺点,将介绍一种改进的算法SCL译码。SCL译码算法中L表示路径搜索宽度,是算法的一个重要参数。SCL算法的思想是:在路径搜索宽度不大于L的情况下,尽可能保留所有可能的译码路径。例L=4如图5。
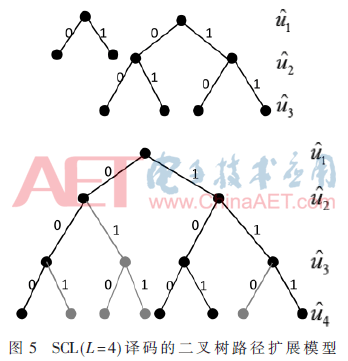
由图5所示在译码进行过程中,每一次判决译码时进行软判决,一条路径会扩展出两条支路0和1。由于在这两条支路所对应的数据是父节点对应的LLR值和部分和的数据内存,所以在这两条支路继续往下延伸时需要把父节点的数据复制到两条支路之一,以保持两条支路拥有独立的数据内存,这样才能使两条支路独立地继续向下延伸。当译码器在译码过程扩展出的路径超过L时,就需要对这些路径进行删减以保证所保留的译码路径不超过L条。图5中L=4,可知译码结束时,会产生4条路径,每条路径对应如图4所示的数据结构。因此在SCL算法中还需要一个参数来度量当路径超过L时哪一条路径需要删除和决定哪一条路径作为最终译码输出结果,这个参数叫作路径度量值(Path Metrics,PM)。PM值是根据决策层的LLR值计算得出的,计算公式如下:

纵观整个SCL译码算法,可知它的核心算法是SC译码,在SCL算法中每一条译码路径都相当于一个SC译码而且都是独立运行的,所以路径扩展时需要进行中间层LLR值和部分和值数据的复制,以保证每条路径能够顺利的进行计算译出对应的码子结果,然后根据路径度量值选出最优的一条路径作为最终的译码输出。特别地,L=1相当于SC译码算法。
3 译码算法优化
3.1 SCL-CRC算法
为了更好地提升极化码译码性能,在进行编码前加入循环冗余校验码(Cyclic Redundancy Check,CRC)。在加入CRC后,在SCL译码最后的路径选择输出码子时可以优先检查CRC的正确性,再考虑PM值的大小。虽然加入CRC校验码(一般为24位)之后,编码的冗余度略增加,编码率由k/N略下降为(k-24)/N,但随着码长增加越不明显。在显著提升译码性能的前提下,显然这点代价是可以付出的。
3.2 “Lazy Copy”算法
在SCL译码算法中,为了使每条译码路径能够独立地进行SC译码,在路径扩展时需要进行数据的复制。但是,通过对SC译码算法的计算方式的分析,得知这些数据不一定需要进行全部复制。比如由图3所示,在判决出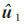 的值完成之后应该判断
的值完成之后应该判断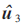 值时,只需要让在计算
值时,只需要让在计算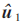 对应的节点的LLR值时所得到节点5、 7的LLR参与计算,即可得出
对应的节点的LLR值时所得到节点5、 7的LLR参与计算,即可得出 对应节点的LLR值。实际上,SCL译码算法在码长和L的值较大时,采取多条路径对应数据进行全部复制在硬件难以实现,因此可以在复制数据时根据计算需要,只复制数据的地址以减轻复制的数据量。在新的路径中需要数据参与计算时可直接通过先前复制的地址直接去寻址得到数据,在部分和的数据的复制上也可以采取同样的方式,这种方法可称之为“Lazy Copy”。这种算法大大减小了SCL译码算法在硬件实现中的功耗和存储需求,提高了译码算法的可实现性。
对应节点的LLR值。实际上,SCL译码算法在码长和L的值较大时,采取多条路径对应数据进行全部复制在硬件难以实现,因此可以在复制数据时根据计算需要,只复制数据的地址以减轻复制的数据量。在新的路径中需要数据参与计算时可直接通过先前复制的地址直接去寻址得到数据,在部分和的数据的复制上也可以采取同样的方式,这种方法可称之为“Lazy Copy”。这种算法大大减小了SCL译码算法在硬件实现中的功耗和存储需求,提高了译码算法的可实现性。
4 仿真分析
Polar Code算法仿真平台是基于AWGN信道下,采用码长N=1 024,码率R=0.5,24位CRC码,分别仿真了L=1,2,4,8,16,32的SCL译码算法性能。仿真结果如图6。
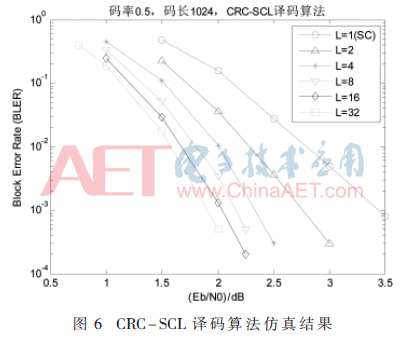
仿真结果表明,随着L的值的增加,误码率越低。由L=1和L=2的性能曲线可以看出,SCL译码算法的性能明显优于SC(L=1)算法的性能。
5 结语
极化码是信道编码领域中唯一被严格证明能够达到香农极限容量的编码技术,目前在国际上也是研究的热点,优秀的性能也使它有望成为5G移动通信系统中新型编码体制的有力竞争方案之一。本文通过对极化码编码和解码的详细剖析,可知无论是编码还是解码在算法上都有很大的研究空间。比如,虽然SCL译码与SC译码相比性能上有了很大的改善,但是算法的复杂度也由此增大。如何设计出更低复杂度更高效的译码算法也是学者们研究的方向之一。
参考文献
[1] SHANNON C E.A mathematical theory of communication[J].Bell Syst Tech,1948,27(03):379-423,623-656.
[2] ARIKAN E.Channel polarization: a method for constructing capacity achieving codes for symmetric binary input memoryless channels[J].IEEE Trans Inf.Theory,2009,55(7):3051-3073.
[3] TELATAR E.Polar Coding:a brief tour[C].USA:IEEE,2010:1-2.
[4] RYUHEI M,TOSHIYUKI T.Performance and construction of polar codes on symmetric binary-input memoryless channels[C].USA:IEEE,2009:1946-1500.
[5] ARIKAN E.Channel combining and splitting for cut of rate improvement[J].IEEE Trans.Inf.Theory,2006,52(02):628-639.
[6] 王东学,宋雷,张士伟.极化码SC译码算法的设计[J].电光系统,2014(3):10-13.
[7] HUANG Z L,DIAO C J,CHEN M.Latency reduced method for modified successive cancellation decoding of polar codes[J].Electronics Letters,2012,48(23):1506-1506.
[8] 李纯,童新海.极化码序列连续删除译码算法的改进设计[J].通信技术,2015(1):19-22.
[9] TAL I,VARDY A.List decoding of polar code[C].USA:IEEE ISIT 2011,2011:1-5.
[10] NIU K,CHEN K.Stack decoding of polar codes[J].Electronics Letters,2012,48(12):695-697.
[11] NIU K,CHEN K.CRC-Aided decoding of polar codes[J].IEEE Communications Letters,2012,16(10):1668-1671.

