高宇航

　　（南京邮电大学 计算机学院，江苏 南京 210003）

        摘要：BP神经网络目前被广泛应用,但是其收敛速度慢、预测精度不高的缺点却一直被人所诟病，因此，在传统BP神经网络中使用附加动量项法以及动态学习速率法，并以两者的融合为基础提出了陡峭因子可调激活函数法来改进BP神经网络。以非线性函数拟合为实例，从收敛速度和预测精度两方面对比分析两种方法，实验证明所提出的改进方法明显提高BP神经网络的收敛速度以及精度。

　　关键词：BP神经网络；附加动量项；动态学习速率；陡峭因子可调激活函数

　　中图分类号：TP183文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.06.017

　　引用格式：高宇航. 一种改善BP神经网络性能的方法研究［J］.微型机与应用，2017,36（6）：53-57,61.

0引言

　　人工神经网络(Artificial Neural Network, ANN)是一种以信息处理的方式对人的大脑神经元网络进行模仿、简化并简单抽象，而非精确逼真地描述的一种非线性动态系统。BP(Back Propagation)神经网络是一种信号正向传播、误差反向传播的多层前馈网络［1］，BP神经网络模型结构如图1所示。

　　由于BP神经网络具有自适应、自组织、实时学习的特点，目前被广泛应用于模式识别、自动控制、预测估计、信号处理、专家系统等领域。但因为其学习规则是基于梯度下降算法，因此就会存在着诸如收敛速度较慢、预测精度不高、不能到全局最小点(即易陷入局部最小点)等问题［2］。所以如何有效地改进BP神经网络成为一个值得研究的重要问题。研究表明影响BP神经网络性能的因素有很多，本文从其中几个方面展开来探究改进BP神经网络的方法。

1BP神经网络的改进

　　1.1附加动量项方法

　　BP神经网络从网络误差的负梯度方向修正权值和阈值，这个过程中并没有考虑以前经验的积累，从而造成震荡的趋势和陷入局部极小值的可能性［3］。因此本文提出采用附加动量项，即在误差的反向传播的过程中给当前权值附加一个与之前一次权值变化量相关的值。附加动量的权值公式为：

　　w(n)=w(n－1)+Δw(n)+η［w(n－1)－w(n－2)］(1)

　　式中，w(n)、w(n－1)、w(n－2)分别表示n、n-1、n-2时刻的权值，η代表动量的学习率。

　　1.2动态学习速率法

　　传统BP神经网络采取固定学习速率η，取值范围一般为［0,1］，如果η选择过小，则会导致学习时间过长;如果η选择过大，虽然可以加快学习速率，但会使权值修改过程产生震荡现象，以致全局误差达不到期望值。

　　为了改进以上问题，根据梯度下降法逼近极小点的路线是锯齿状的、越靠近极小点收敛速度越慢的特征，提出动态学习速率法来达到缩短训练时间的目的。具体步骤如下: 首先设置初始学习速率η，然后检查修改之后的权值能否减小误差，如果可以，则说明学习速率设置较小，需要加大学习速率η；如果未能减小误差，则说明调整过度，需要降低学习速率η。将对动态学习速率η的调整公式定义如下：

　　η(n+1)=1.04η(n)，Ε(η+1)<Ε(η)

　　0.6η(n)，Ε(η+1)>1.03(η)

　　η(n)，其他情况（2）

　　1.3选择适当的激活函数

　　在神经网络中，一个神经元的激活函数是用来执行复杂的映射功能，其决定了这个神经元节点的输出［4］。FESAURO G指出BP神经网络的收敛速度受激活函数直接影响［5］。

　　激活函数的作用主要体现在为多层神经网络引入非线性因素［6］。因为线性模型的表达能力是十分欠缺的，倘若神经网络中全是线性部件，输出都是输入的线性组合，与没有隐层效果相当，这种情况就是最原始的感知机（Perceptron）。非线性是神经网络的核心，一旦引入了非线性，BP神经网络就可以有效地逼近任意连续函数，能够解决线性模型所不能解决的非线性问题［7］。

　　目前常用的激活函数有Sigmoid函数和双曲正切函数两种。

　　（1）Sigmoid函数： Sigmoid函数的函数图形为s形，函数定义为：f(net)=11+e－net，它是一种有界可微的实函数，在每一点导数的值始终是正数，其导数为:f′(net)=e－net(1+e－net)2。Sigmoid函数图像及其导数图像如图2所示。

　　它的输出范围有限，可以将输入的数值映射到0和1之间，所以数据在传递过程中不易发散。函数趋向于负无穷时极限为0，函数趋向于正无穷时极限为1。 Sigmoid函数可以轻而易举地将非线性引入到网络中［8］。但是Sigmoid函数也有着如下两个较为致命的缺点：

　　①饱和时梯度消失。当输入值很大或很小的情况下，Sigmoid函数的这些区域的梯度几乎为0，即梯度消失。而对于BP神经网络而言，如果梯度过小的话，则会导致权值的修改量很小或者几乎为0，从而导致整个网络难以学习。

　　②Sigmoid函数的输出值不是零均值化的。这会导致下一层神经元将本层非零均值化的输出信号作为输入。试想一下如果数据输入神经元是恒正的,那么所得出的梯度也会是恒正的数，而从产生锯齿现象而导致收敛速度变慢。

　　（2）双曲正切函数：又称为Tanh函数，其函数可以表达为：f(net)=21+e－2net－1，其导数为：f′(net)=1－f(net)2。Tanh函数图像及其导数图像如图3所示。可以将输入的数值映射到-1与1之间，图像过原点且穿越I、III象限，Tanh函数是一个严格单调递增函数。函数趋向于负无穷时极限为-1，函数趋向于正无穷时极限为1［9］。Tanh函数针对Sigmoid函数输出值非零均值化做出了改进，但是饱和时梯度消失的问题依旧存在［10］。

　　为了对比Sigmoid函数与Tanh函数作为激活函数的性能，以经典非线性问题——异或问题（XOR）作为研究对象，分别用两种函数作为激活函数，将最大训练次数设为1 000次，训练的预期均方误差(MSE)精度设为0.000 1，Sigmoid与Tanh的迭代次数对比如表1所示。表1Sigmoid与Tanh的迭代次数的对比激活函数SigmoidTanhMSE精度0.000 10.000 1实际MSE精度0.000 094 5460.000 091 367迭代次数10720

　　根据表1可以得知，Tanh函数作为激活函数时BP网络的收敛速度要优于Sigmoid作为激活函数的收敛速度，其性能大约为Sigmoid的5倍。

　　1.4改进激活函数

　　传统BP神经网络中，只有连接神经元之间的权值以及作用在激活函数上的阈值是可调整的，而激活函数则是固定不变的，这样一来就制约了BP神经网络的非线性映射能力，继而影响网络的精度以及收敛速度［11］。为了改进上述问题，有学者提出了针对Sigmoid函数的垂直、水平位置的改进［12］，但是根据上文可以得知Tanh函数作为激活函数要优于Sigmoid函数，BP神经网络学习规则是基于梯度下降法的特征以及实际上激活函数的性能与函数的陡峭程度的关联更紧密的结论［1314］，在为了达到优化BP神经网络的同时，没有必要将其变得更加复杂。基于以上思想本文提出如下形式的陡峭因子参数可调Tanh函数：

　　f(net)=21+e－2αx－1（3）

　　其中，α为陡峭因子，其决定函数的陡峭程度。本文中xj代表输入层的第j个节点的输入，假设输入层有m个节点，那么j=1,…,m;wji为输入层第j个节点到隐层第i个节点之间的连接权值；ψi表示隐层第i个节点的阈值；f1(α1 net)为隐层的激活函数，其中α1是隐层激活函数的可调节陡峭因子；win代表隐层第i个节点与输出层第n个节点之间的连接权值，假设隐层存在q个节点，则n=1,…,q；θn表示输出层第n个节点的阈值；f2(α2net)为输出层的激活函数，α2是输出层激活函数的可调节陡峭因子；on代表输出层第n个节点的输出，假设输出层存在l个节点，n=1,…,l。

　　根据以上规定，改进之后的BP神经网络的前向传播过程为：

　　隐层第i个节点的输入为：

　　neti=∑wjixj－ψi（4）

　　隐层第i个节点的输出记为：

　　yi=f1(α1neti)=f1(α1∑mi=1wjixj－ψi)（5）

　　输出层第n个节点的输入为：

　　netn=∑qn=1winyi－θi=∑qn=1winf1(α1∑mi=1wjixj－ψi)－θi（6）

　　那么，输出层上第n个节点的输出值就可以用以下形式表示：

　　on=f2(α2netn)=f2(α2∑qn=1winyi－θi)=f2∑qn=1winf1(α1∑mi=1wjixj－ψi)－θi（7）

　　改进之后的BP神经网络误差的反向传播过程如下：

　　每个样本p的二次型误差准则函数为：

　　Ep=12∑ln=1(tn－on)2（8）

　　设系统中共有P个训练样本，则系统总误差准则函数为：

　　E=12∑Pp=1∑ln=1(tn－on)2（9）

　　根据BP神经网络反向传播的原理，为了使得连接权值沿着E的梯度下降的方向改善，需要依次计算Δwin、Δwji、Δα2、Δα1，可以利用以下公式来计算出需要的值，其中η为增益因子。

　　改进之后的BP神经网络的输出层权值调整公式为：

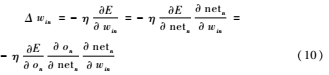
　　改进之后的BP神经网络的隐层权值调整公式为：

　　改进之后的BP神经网络的输出层激活函数陡峭因子调整公式为：

　　改进之后的BP神经网络的隐层激活函数陡峭因子调整公式为：

　　根据求导法则，可以求得：

　　

　　经过整理，最后得到如下公式：

　　最后将计算出的值带入如下更新公式中，其中t表示某一时刻：

　　win(t+1)=win(t)+Δwin（17）

　　wji(t+1)=wji(t)+Δwji（18）

　　α2(t+1)=α2(t)+Δα2（19）

　　α1(t+1)=α1(t)+Δα1（20）

2实验结果与分析

　　为了验证改进之后BP神经网络的性能，使用MATLAB工具对非线性函数z=x2+y2进行拟合，从其1 800组输入输出数据中随机选取1 700组作为训练数据，用于BP神经网络的训练，剩余100组作为测试数据用来测试网络的拟合性能［15］。

　　分别对采用Tanh函数作为激活函数的传统BP神经网络以及采用附加动量项方法与动态学习速率及参数可调Tanh激活函数结合的方法改进的算法对网络进行训练，最后对两种方法的结果进行比较分析。

　　2.1网络初始化

　　在网络初始化阶段需要确定输入层神经元节点的个数nI、输出层神经元节点的个数nO、隐层神经元节点的个数nH。根据需要拟合的非线性函数的特征，将输入层神经元节点个数nI设定为2，输出层神经元节点个数nO设置为1， 隐层神经元节点个数nH可根据如下公式得到：

　　nH=nI+nO+a

　　其中a为0~10之间的常数。根据以上设定，最终构造的BP神经网络的输入层神经元节点个数为2，隐层神经元节点个数为10，输出层神经元节点个数为1。接下来则需要对网络参数进行随机初始化：连接权值∈（-0.5，0.5）；阈值∈(-0.5,0.5)；陡峭因子∈（0.7，1.5）。

　　2.2数据预处理

　　参数随机初始化之后，需要对待输入至网络中的数据进行归一化处理，这样可以减小各维数据间数量级的差别，从而避免因为输入输出数据数量级差别较大而造成网络收敛慢、训练时间长的问题。

　　MATLAB中对应归一化代码如下：

　　［inputn,inputps］=mapminmax(input_train);

　　［outputn,outputps］=mapminmax(output_train);

　　2.3对比试验

　　针对传统BP神经网络以及采用附加动量项方法与动态学习速率以及参数可调Tanh激活函数结合的方法改进的网络分别进行训练，指定训练的目标均方误差分别取值为0.000 01与0.000 001，最大迭代次数设置为10 000次。

　　最后，以100组作为测试的数据分别针对迭代次数与误差精度两个方面来分析传统BP神经网络与改进后的BP神经网络的拟合性能，结果如下。

　　从迭代次数的角度来分析，如图4与图5所示，当系统目标均方误差设置为0.000 01时，传统BP神经网络到达该精度需要迭代70次，而改进之后的BP神经网络只需要迭代33次就能达到该精度。

　　系统目标均方误差为0.000 001时，如图6与图7所示，该精度要求下传统BP神经网络迭代了193次才完成，反观改进后的BP神经网络则只用迭代72次就轻松的达到了均方误差精度的要求。

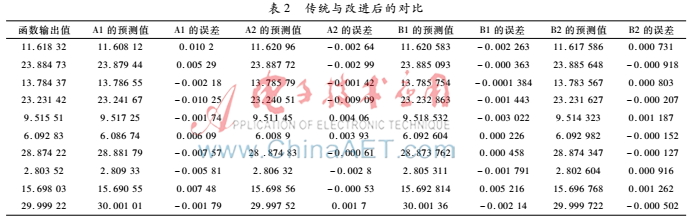
　　接着，从学习精度方面来分析。限于篇幅，从100个测试数据中随机抽取出10个数据作为样本，将目标均方误差精度为0.000 01时传统BP神经网络的预测值记为A1，改进后的BP神经网络记为A2；将目标均方误差精度为0.000 001时传统BP神经网络的预测值记为B1，改进后的BP神经网络记为B2，结果的表2所示。从表2可以观察出改进后的BP神经网络较之于传统神经网络在学习精度方面亦有着较为明显的改善。

3结论

　　针对传统BP神经网络收敛速度较慢、预测精度不高、极易陷入局部最小点的缺点，本文提出了一种将平滑权值变化的值附加动量项方法与动态学习速率方法以及陡峭因子参数可调激活函数结合起来的改进方法，并与传统BP神经网络进行了以非线性函数拟合为实验的对比分析，证明了本文改进的BP神经网络具有更快的收敛速度以及更高的精度。

　　参考文献

　　［1］ 周志华，曹存根. 神经网络及其应用［M］. 北京：清华大学出版社，2004.

　　［2］ ABRAHAM A. Meta learning evolutionary artificial neural networks［J］. Neurocomputing, 2004, 56: 1-38.

　　［3］ 张雨浓, 曲璐, 陈俊维, 等. 多输入 Sigmoid 激励函数神经网络权值与结构确定法［J］. 计算机应用研究, 2012, 29(11): 4113-4151.

　　［4］ Wu Ailong, Zeng Zhigang. Global exponential stability in Lagrange sense for periodic neural networks with various activation functions ［J］. Neurocomputing, 2011, 74(5):831-837.

　　［5］ DEBES K, KOENIG A, GROSS H M. Transfer functions in artificial neural networksa simulationbased tutorial［J］. Brains, Minds and Media, 2005(1).

　　［6］ MHASKAR H N, MICCHELLI C A. How to choose an activation function［J］. Advances in Neural Information Processing Systems, 1994: 319.

　　［7］ GULCEHRE C, MOCZULSKI M, DENIL M, et al. Noisy activation functions［J］. arXiv preprint arXiv:1603.00391, 2016.

　　［8］ 王雪光, 郭艳兵, 齐占庆. 激活函数对 BP 网络性能的影响及其仿真研究［J］. 自动化技术与应用, 2002,21(4): 15-17.