宋洪宇,史小宏

　　(上海海事大学 信息工程学院，上海 201306)

　　摘要：为了解决复杂系统的可靠性和任务成本评估问题，提出混合冗余备用系统设计模式。通过概率统计分布方法来计算复杂系统元件的可靠性和任务成本，利用蚁群和遗传相结合的混合算法来解决备用元件的最优分布问题。最后通过仿真实验计算出系统的可靠性和任务成本，以及备用元件的优化分布序列，在满足一定的系统可靠性的基础上使得备用元件的操作成本最小化。

　　关键词：冗余备用；可靠性；任务成本；蚁群遗传算法；最优分布

　　中图分类号：TP302.8文献标识码：ADOI： 10.19358/j.issn.1674-7720.2017.10.012

　　引用格式：宋洪宇,史小宏.基于蚁群遗传算法的冗余备用元件优化研究［J］.微型机与应用，2017,36（10）：40-43，47.

0引言

　　复杂系统在工作中时常会出现故障，为了保障其可靠性，其中一个广泛使用的技术就是冗余备用［1］：一个或多个元件处于工作状态下，当有一个正在工作的元件出现故障的时候，就会有一个备用元件被激活来替换这个出现故障的元件，保证系统能够继续运行下去。常用的冗余类型有热备份和冷备份［2］，当元件处于热备用模式下的时候，一旦工作中的元件出现故障，热备用元件可以提供快速恢复。为了确保系统能够随时替换出现故障的工作元件，就需要时刻补充热备用模式下的元件。由于热备用中的元件一直处于工作中，这就增加了系统的成本开销和能源消耗，与此相比，处于冷备用模式下的元件是低成本的，但是当它去替换工作中失效的元件时，需要长时间的恢复延迟。

　　考虑到冷热备用各自的优缺点，提出混合冗余备用系统模式，即让较少的元件处于热备用模式下，可以随时快速地替换出现故障的工作元件，让大部分元件处于冷备用模式下，当热备用模式下的元件用完后，处于冷备用模式下的元件会转移到热备用模式下［3］。这种冗余备用模式不仅保留了热备用模式快速替换的特点，还大大提高了系统的可靠性，与此同时，处于冷备用模式下的元件运行成本低，又大大降低了系统的成本开销。

　　最后，当冗余元件满足系统可靠性时，使用离散数学的概率分布方法来计算系统可靠性和预期任务成本。冗余备用模式下的元件分布和启动顺序对系统的可靠性和成本会产生严重的影响［4］，利用蚁群遗传混合算法来优化冗余备用模式下的元件，分析备用元件在冗余模型中的不同分配对系统可靠性和预期任务成本的影响，并找出最优元件分布和初始化顺序［5］。

1元件的混合冗余备用模型

　　假设系统中有N个独立的备用元件s(1),s(2),…，s(N)，让H个备用元件处于热备用模式下，当系统开始运行的时候，对s(1),s(2),…，s(H)进行了初始化，剩下的N－H个备用元件s(H+1),…,s(N)处于冷备用模式下。

　　当系统中运行的工作元件失效时，处于热备用模式下的元件会立刻替换失效元件；当热备用模式下的元件用完后，处于冷备用模式下的元件进行初始化。

　　为了方便求得系统可靠性，提出一些附加假设：

　　（1）系统中的元件数量和类型是固定的；

　　（2）元件之间相互独立；

　　（3）和任务时间相比，替换失效元件的时间可以忽略不计；

　　（4）工作中的元件和备用元件的失效是不可修复的。

　　1.1故障元件概率计算

　　将整个运行时间t分成m个相同的时间单元，即Δ=t/m，备用元件k在第i个时间单元失效的概率为pk(i)，每个备用元件有相同的累计失效分布函数Fk(t)。假设指数分布的时间失效率为λk，那么

　　Fk(t)=1－exp(－λkt)（1）

　　pk(i)=［1－exp(－λkΔ)］exp(－λkΔi)（2）

　　根据韦伯分布提供的规模参数ηk以及状态参数βk，得到的分布函数和概率密度函数公式如下：

　　Fk(t)=1－exp(－(t/ηk)βk)（3）

　　pk(i)=exp{－［Δi/ηk］βk}－exp{－［Δ(i+1)/ηk］βk}（4）

　　考虑到备用元件的失效分布时间Tk是离散的而不是连续的，假设Tk的概率质量函数用向量表示为pk={pk(0),…,pk(m)}，pk(i)=Pr{Δi≤Tk<Δ(i+1)}(0≤i<m），pk(i)表示备用元件k在第i个时间间隔失效的概率。

　　由于系统元件的运行时间不会超过任务时间t，在整个任务结束之前元件k不会失效的概率为：pk(m)=Pr{Tk≥t=Δm}就可以表示为：

　　1.2系统元件的失效时间分布

　　根据前面给出模型的描述可知，当k=H+1时，说明热备用模式下的元件已经用完，系统中冷备用模式下的元件在第k－1个元件出现失效时便进行初始化。当系统中第k个备用元件从运行时间开始到间隔Xk发生失效时，向量为Qk=(Qk(0),…,Qk(m))，可知，Qk(i)=Pr{Xk=Δi}。若备用元件s(1)在运行时间开始时进行初始化，便有X1=Ts(1)和Q1(i)=ps(1)(0≤i≤m)。热备用模式下的冗余元件在运行时间开始时便进行初始化，可知Xk=max(Xk－1,Th(k))，那么热备用模式下的冗余元件可靠性公式为：

　　当热备用模式下的元件全部使用完或发生失效时，处于冷备用模式下的元件便会进行初始化，可知Xk=Xk－1+Th(1)，冷备用模式下的元件可靠性公式有：

　　Qk(i)=∑ij=0Pr{Xk－1=Δj}Pr{Th(k)=Δ(i－j)}

　　=∑ij=0Qk－1(z)ph(k)(i－j)（7）

　　Qk(m)=∑m－1j=0Pr{Xk－1=Δj}∑mn=m－jPr{Th(k)=Δn}

　　=∑m－1j=0Qk－1(j)∑mn=m－jph(k)(n)（8）

　　1.3系统可靠性和预期成本计算

　　根据上面的研究工作，备用元件的系统可靠性和预期成本评估算法如下：

　　C=R=0,Q0(1)=1,Q0(i)=0(2<=i<=m)

　　for k=1,…,H

　　set Qk(j)=0(1<=j<=m)

　　C=C+Vh(k)

　　for i=0,…,m;C=C+△*i*w h(k)*p h(k)(i)

　　for z=0,…,m-1

　　for i=0,…,m

　　j = max(z,i)

　　Qk(j)=Qk(j)+Q k-1(z)*p h(k)(i)

　　R=R+Qk(m)

　　for k=H+1,…,N

　　set Qk(j)=0(0<=j<=m)

　　C = C+V h(k)(1-Q k-1(m))+△*m*

　　W h(k)*Q k-1(m)

　　for i 0=0,…,m-1

　　C = C+△*i0*W h(k)*Q k-1(i0)

　　fori=0,…,m

　　j =i +i0

　　if (j>m) j=m

　　C=C+△*(j-i0)*w h(k)*Q k-1(i0)*

　　p h(k)(i)

　　Q k(j)=Q k(j)+Q k-1(i0)*p h(k)(i)

　　R = R + Q k(m)

2蚁群遗传算法元件优化

　　2.1蚁群遗传算法的思想

　　遗传算法［6］具备全局搜索能力，能够迅速地搜索出解空间中的全部解，通过其内在并行性进行分布式计算，求解速度明显加快。缺点是没有很好地使用系统反馈回来的信息，使搜索产生盲目性，降低了最优解的收敛速度，致使计算最优解效率较低。蚁群算法［7］是一种基于种群的优化算法，它由多只蚂蚁共同构建解路径，该算法根据在解路径上遗留且互换信息素来实现优化过程，提高了解路径的效率。拥有正反馈机制，利用信息素的持续变化以及收敛得到优化解。然而，由于缺少初始信息素，因此信息的积累过程比较耗时。

　　蚁群遗传算法［89］就是把蚁群算法和遗传算法组合起来，把遗传算法引入到蚁群算法迭代中，把遗传算法每一次父类计算生成的解当成蚁群算法的初始群体，根据蚁群算法的多次循环，加快收敛速度，提高求解效率并找到最优解［10］。本文采用遗传算法进行遗传算子操作，生成合适的解作为蚁群算法的初始信息素，利用蚁群算法进行蚂蚁路径转移和信息素的更新［11］，获得最优解。

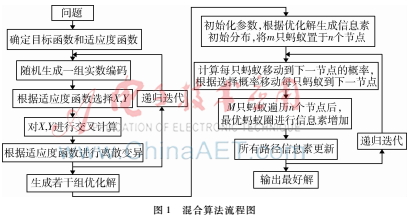
　　2.2蚁群遗传算法的优化过程

　　（1）定义目标函数和适应度函数，计算每个个体的适应度fi，对种群规模中的个体进行如下遗传操作，从而产生下一代个体。

　　①选择算子，使用遗传算法中的轮盘赌方法，种群中个体适应度函数值越大，被选择的机率就越高。

　　②交叉算子，利用实数编码，交叉操作使用算术交叉算子，首先随机确定参与交叉的父代，接着进行两两配对，父代中的个体X和Y按照式(9)产生两个新的个体:

　　X′=eX+(1－e)Y

　　Y′=(1－e)X+eY′（9）

　　其中e∈(0,1)

　　③变异算子，采用离散突变算子［12］，用特定概率对父代中每个个体进行变异，返回突变后的个体并放入新种群中。

　　(2)反复执行选择、交叉、变异操作，直至达到遗传算法结束前提。假定最少循环次数为Nmin，最多循环次数为Nmax，在遗传算法的迭代过程中计算进化率，公式如下:

　　f-=(fn－fn－1)/∑ni=1fi（10）

　　如果持续三次进化速率不大于最小进化速率，则结束遗传算法的循环，开始执行蚁群算法。

　　（3）当遗传算法运行完毕后，将产生的适应度强的后代加入到新组合中。

　　（4）依据优化解得出吸引强度初始分布，使用蚁群算法信息素的初始值设定方法，求出其信息素初始值τ，有τ=τc+τg，其中τc表示给出的信息素常量，τg表示遗传算法求得结果转换的信息素值。

　　（5）m只蚂蚁被放置在它们各自的初始节点上，计算每只蚂蚁从i节点移动到j节点的移动概率pm(i,j），依据移动概率转移每只蚂蚁到下一节点，并且执行信息素局部更新。

　　（6）判断所有蚂蚁是否已生成整个路径［13］，若还没有生成整体路径则执行步骤（5），否则，执行步骤（7）。

　　（7）比较所有的可行解, 输出最优解。

　　整个过程的流程图如图1所示。

　　由于备用元件的初始化顺序强烈地影响着系统的可靠性和预期任务成本，接下来要解决的问题就是找出混合冗余备用元件的最优分布序列，当达到相应可靠性级别R*时，使得系统的花销最小化。

　　min C s.t R≥R*(11)

　　将备用元件的初始化序列用染色体来表示，寻找存在于热备用模式和冷备用模式下的冗余元件，根据前面求可靠性和任务成本的计算方法，能够得出系统中备用元件按照相应顺序时的可靠性R和预期任务成本C，接下来再根据公式(11),先设定Ω=M-C-σmin{0,R*－R}，其中M是一个非常大的整数，通过此式来解决系统冗余元件的优化分布问题,当σ=0时，能够计算出系统最小任务成本开销，当σ变大且R*=1时，就变成了计算系统元件的最大可靠性问题。

　　当蚁群遗传算法进行时，从0~N的随机数字中选择一组数据组合作为解决方案，任意生成的集合表示系统中冗余备用元件的初始化序列，例如{3,1,4,6,2,5}这组数字组合，3,1,4表示热备用冗余元件的初始化序列，利用遗传算法交叉和变异的手段得到新的解决方案，进而求出适应度函数值，接着把求得的初始化序列放入到上一节的可靠性和任务成本计算方法里，得出这种状况下的可靠性和预期任务成本，并带入公式(11)中去判断得出的适应度函数值是否满足需求，然后根据蚁群算法信息素的初始值设定方法，求出其信息素初始值并进行信息素局部更新，获得新的个体保留最优解，直到蚁群遗传算法计算出一组元件初始化列表，当求出的系统可靠性满足公式(11)时，蚁群遗传算法终止，保留最优解情形下的备用元件的初始化列表。

3仿真结果与分析

　　3.1模拟计算结果与分析

　　本节通过仿真实验来实现模型，假定一个复杂多态系统中含有6个备用冗余元件，系统中元件的失效状态能够使用韦伯失效分布模型来表述，表1提供了韦伯规模参数ηk和状态参数βk。此外，表1还提供了冷备用和热备用模式下的冗余元件的启动开销，设定系统的总运行时间t=300，当m=500时，前面三个备用元件放置在热备用模式中，后面三个备用元件放置在冷备用模式中，那么根据前面的估算方法就能够得出系统的任务成本开销C=21 476和可靠性R=0.956 2。

　　接下来研究时间单元m对系统可靠性和预期成本的影响，将三个备用元件放置在热备用模式下，其余三个备用元件放置在冷备用模式下，根据图2能够得出不同时间单元对可靠性和预期成本的影响。

　　3.2元件最优分布与初始化顺序

　　设定有8个备用元件存在于系统中，根据表1提供的各种参数以及模型中的可靠性与成本估算方法，采用蚁群遗传混合算法进行优化处理，能够获得系统中备用元件的最优序列分布，并且随着遗传迭代的改变，最优解越来越趋于稳定，如图3所示。

　　同时能够求出在达到不同的可靠性级别R*的时候，设置蚁群算法初始值信息素τc为20，遗传算法进入到蚁群算法的信息素强度值τg为2，蚂蚁数量为6，采用蚁群遗传算法得出复杂系统的可靠性和预期任务成本以及备用元件的初始化序列，如表2所示。　

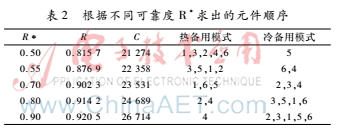
　　最后得出不同的可靠性与预期任务成本的一个平衡趋势曲线，如图4所示。这种平衡趋势曲线能够协助复杂系统的混合冗余备用模型的设计，并且可依据对成本和可靠性的需要来分配备用元件。

4结论

　　本文针对系统中工作的元件遇到故障不可修复的情况，设计了一种混合冗余备用模型，根据概率分布的计算方法，通过仿真实验来计算得出混合备用模式下系统的可靠性和预期运行成本，提出了基于蚁群遗传混合算法对系统中冗余备用元件的分布进行处理和优化的方案，找到了在满足一定可靠性和预期任务成本的条件下，系统中备用元件的一组初始化序列，为系统元件分布和优化提供了依据。

参考文献

　　［1］ 刘士喜,许志才,方贤文.基于随机Petri网的冗余备份系统可信赖性研究［J］.安徽理工大学学报(自然科学版)，2009,29(3):48-53.

　　［2］ 黎邵平,李锡文.双机热冗余控制系统的可靠性分析［J］.自动化技术与应用，2006,25(12):18-20.

　　［3］ LEVITIN G,Liu Dongxing,Dai Yuanshun.Reliability and mission cost of 1outof N:G systems with statedependent standby mode transfers［J］.IEEE Transactions on Reliability,2015,64(1):454-462.

　　［4］ 杨博文,赵海,刘飞,等.基于可靠度的导弹维修备件需求评估方法研究［J］.微型机与应用,2011,30(4):94-96.

　　［5］ 仲彦军.冷备状态下具有两个状态的由两个相同部件并联的可修系统研究［D］.乌鲁木齐：新疆大学,2006.

　　［6］ 马书南，帅训波，曹凤雪.一种基于逆序算子优化组合遗传算法［J］.电子技术应用,2006，32（6）：19-21.

　　［7］ 程世娟,卢伟,何平.蚁群算法在冗余系统可靠性最优分配上的应用［J］.计算机工程与应用，2009，45(15)：64-66.

　　［8］ 申利民.基于遗传蚁群融合算法的测试用例最小化研究［J］.计算机工程，2012，38(16):57-64.

　　［9］ 姜封国.基于混合遗传算法的随机结构可靠性优化设计［J］.华南理工大学学报,2008，36(1):152-156.

　　［10］ 徐德明.改进的遗传混合蚁群算法在TSP问题中的应用［J］.计算机时代，2012(11)：1-64.

　　［11］ 杨剑峰.基于遗传算法和蚂蚁算法求解函数优化问题［J］.浙江大学学报，2007,41(3): 427-430.