0 引言

    在基于能量获取的协作认知无线电网络中，将拥有频谱资源的授权系统称为主系统，共享主用户频谱资源的系统称为次级系统。目前基于能量获取的协作认知通信受到越来越多的关注^[1-3]。文献[1]研究单次用户(Secondary User，SU)的最佳决策，先分别在主用户(Primary User，PU)直传和SU参与PU的协作下进行SU的吞吐量的最大化，再根据两种方式下优化后的SU的吞吐量来确定SU的最佳协作策略。文献[2]利用猫群算法在不影响PU的基本性能情况下，最大化SU的吞吐量。文献[3]针对PU和SU的非饱和数据传输问题，构建排队论的模型，通过求解“概率协作”策略中SU的传输概率，从而最大化SU的服务率。

    对比现有工作并基于以上的考虑，本文在无线能量获取的协作认知网中，通过次用户对主用户的贡献程度来分配时隙，从而调动了次用户的积极性，并选取最佳的次用户集合，并对其进行资源分配，从而最大化次用户系统的吞吐量。

1 系统模型和问题描述

1.1 系统模型

    系统结构如图1所示，在该网络中，次用户由拥有足够能量的混合接入接点（HAP）供能。次用户（SU）协助主用户（PT-PR）传输信息，作为回报，次用户可以获得一定的传输时间传输自己的数据。系统的帧时隙如图2所示，总时隙为T，分为四个阶段：

    (1)阶段I：当主链路直传时，SUS从HAP广播的射频信号中获取能量，用于数据传输，时隙为t_e；

1.2 问题描述

    在整个时隙T内，主用户满足最基本的速率R_p：

    SUS消耗的能量要小于获取的能量，因此每个SU_i满足下列条件：

    由式(4)可以看出，次用户系统对主用户速率的贡献受h_ipP_ip的影响，因此为了调动次用户协作主用户的积极性，次用户的接入时间可以根据每个次用户的贡献大小来分配：

    由于式(6)、式(8)这两个约束式中存在两个优化变量的相互耦合，且S_D的不确定性，使得式(10)问题无法利用现有的凸优化算法直接求解。为了有效解决这个问题，可先将式(6)转化为：

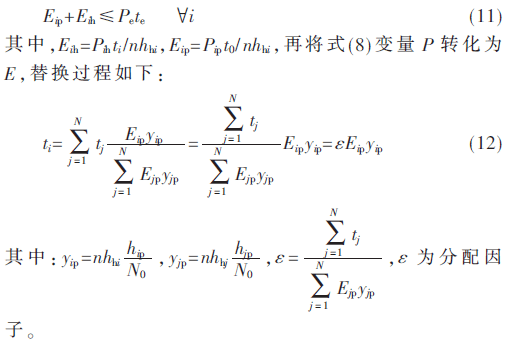
    这样在确定参与协作的SUS和确定ε后，问题(10)可以转化为(13)，该问题是凸优化问题，为了简便，可以将T设置为1：

2 优化问题

2.1 问题（13）的解决——全局变量优化

    令|S_D|=N，并将h_ps=[h_p1，…，h_pN]中的元素大小按递减的顺序排列。按算法1执行该流程。

    算法1：

2.2 对于给定S_D下问题（13）的优化

    (1)首先，保持t_e、ε不变(ε的优化描述)后，将问题(13)转化为2个子问题：S1-固定(t₀)下的(E_sh，E_sp)的能量分配和S2-固定(E_sh，E_sp)下的(t₀)的时隙分配，分别为；

    S1和S2是凸优化问题，满足卡罗需-库恩-塔克(KKT)条件^[4]，可以通过求解它们的对偶问题得到最优时间和能量分配。

    S1的拉格朗日函数为：

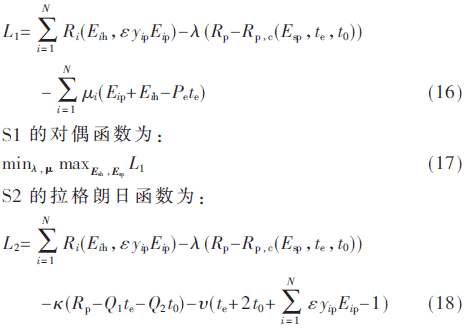
    再对SU_i(i=1，2，…，N)都进行式(16)和式(18)的求解，最佳资源分配式子如下：

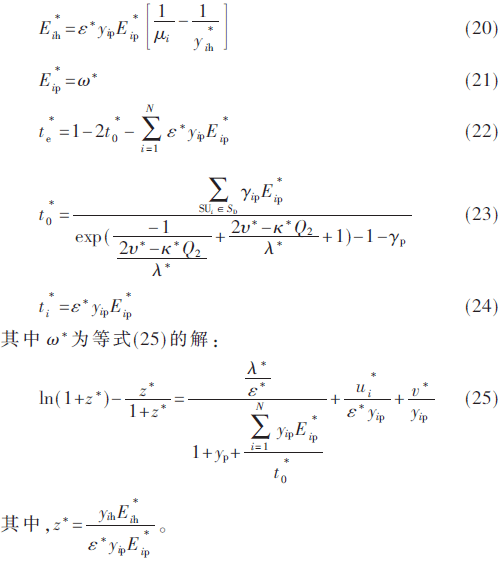
    证明：对 L₁关于(E_ih，E_ip)和L₂关于(t₀)求偏导，让其偏导等于0，联合便可求得。

    (2)接下来对t_e进行梯度更新，t_e的梯度函数为：

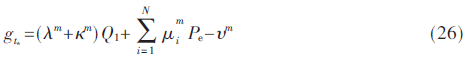
其中m为迭代次数。

    算法2：

3 仿真结果

3.1 仿真参数设置

    本文利用MATLAB对其进行仿真来验证上述的合理性。仿真中，PT、PR、HAP之间连线构成等边三角形，距离都为50 m，SUS随机分布在以HAP为圆心的、r=10 m的圆内。用户i和用户j之间的链路的瞬时信道功率增益表示信道服从瑞利衰落，P_p为20 dBm，能量转换系数n为0.5，噪声功率N₀为-60 dBm。

3.2 仿真结果分析

    图3仿真了R_p和R_s，sum的关系图，由图可知，在相同的R_p条件下，本文比文献[5]达到次用户的速率高，且N越大越明显。这是因为在文献[5]的资源分配中，次系统中次用户虚报自己的资源信息，导致可能选择到信道状况不好的次用户参与到协作，从而造成资源分配不均匀。而在本文中的先根据信道状况的好坏进行排列，再根据次用户的协助主用户的贡献来进行合理资源分配，有效地防止次用户虚报行为，从而比文献[5]更有效地提高次用户系统速率。当R_p达到3时，R_s，sum趋近于0，这是因为为了达到主用户的传输要求，次用户系统资源主要消耗在协作阶段。

    图4仿真了R_p和2t₀的关系图。可以看出，随着R_p的增加，在相同N下，需要次用户系统中继的时间越长；但在相同的R_p的条件下，N越大，相应的中继时间会有所降低，这是因为有了更多的次用户参与。本文的中继时间比文献[5]时间低，这是因为根据次用户协助程度来分配资源，增强了次用户协作的积极性，从而节省中继时间。

    图5仿真了R_p和t_a的关系图，可知，在一定的R_p的范围内，本文的次用户系统所得到的总回报时间t_a比文献[5]的大，这也和图3是对应的，由于本文次用户参与中继时间减少，次用户得到更多的回报。

4 结论

    本文基于能量获取的协作认知网络，对其建模进行分析，次用户通过为主用户服务的协作程度来获得自己传输机会，提高了次用户参与的积极性。最后仿真结果证明，本方案可以更好地提高次用户系统的吞吐量。

参考文献

[1] YIN S，ZHANG E，QU Z，et al.Optimal cooperation strategy in cognitive relay networks with energy harvesting[J].IEEE Transactions on Wireless Communications，2014，13(13)：4693-4707.

[2] Gao Hongyuan，EJAZ W.Cooperative wireless energy harvesting and spectrum sharing in 5G networks [J].IEEE Access，2016，4(6)：3647-3658.

[3] 阔永红，贺冰涛，陈健.携能通信协作认知网络稳态吞吐量分析和优化[J].西安电子科技大学学报，2016，43(6)：1-7.

[4] THOMAS L C.The wijngaard-stidham bisection method and replacement models[J].IEEE Transactions on Reliability，1982，31(5)：482-484.

[5] SAMI M，NOORDIN N K，KHABAZIAN M.A TDMA-based cooperative MAC protocol for cognitive networks with opportunistic energy harvesting[J].IEEE Communications Letters，2016，20(4)：808-811.

作者信息：

杨  路，黄  凯，杨品章

（重庆邮电大学 通信与信息工程学院，重庆400065）