0 引言

    码率为R=(N-M)/N的低密度奇偶校验(Low-Density Parity-Check，LDPC)码是一种线性分组码^[1-2]。LDPC码因其优异的译码性能，已经受到了越来越多的关注，并且日前在深空通信、光纤通信、卫星数字视频、音频广播等领域已经得到了广泛的应用^[3]。

    LDPC码的传统迭代译码算法flooding^[4-6]，又称为两相的消息传递，是最简单的译码方式。flooding算法这种在一次迭代中顺序更新所有节点的方式，导致其译码的收敛速度较慢，并且需要大量的迭代次数才能达到想要的译码效果。为了减少迭代的次数和收敛速度, 时序置信传播译码算法^[7-8]（Belief-Propagation，BP）被提出。在时序译码算法中，假设校验节点被分成p个子集，在一次迭代过程中，第一个子集中从变量节点到校验节点的信息被更新，然后从校验节点到相邻的变量节点的信息要被更新并传播，同样其他p-1个校验节点的子集也同时相应地被更新。很明显，一次迭代过程也涉及到所有变量节点以及所有的校验节点的子集，因此，每次译码迭代，时序译码算法的计算复杂度和传统flooding相同，但是其收敛速度对比flooding算法，要快过两倍。尽管置信传播算法有很好的译码性能，但为了进一步提高译码性能，其不是最好的选择，最终，Casado等人将剩余度概念运用到了置信传播^[9-10]，并提出了两种时序算法：基于剩余度置信(Residual Belief Propagation，RBP)传播译码算法、基于校验节点的剩余度置信传播(Node-Wise RBP，NWRBP)译码算法^[11-12]。

    RBP算法和NWRBP算法这种迭代机制会导致有的变量节点很少有机会去将它们本身的消息传播到整个译码过程中，所以，其译码算法不会达到最好的译码效果。为了减少这种情况带来的误差，本文提出了一种改进型NWRBP(Enhanced NWRBP，ENWRBP)算法，在迭代译码过程中，如果NWRBP算法译码没有成功，则依次将更新最少次数的变量节点的初始化对比似然数值(Log-Likelihood Radio，LLR)设置为0，并重新译码，直到译码正确或达到最大测试次数。本算法最多测试T个变量节点。该算法改变了校验节点的更新顺序，均衡了变量节点的更新次数，从而提高了LDPC码的译码性能。

1 LDPC码的RBP和NWRBP译码算法

    对于规则(N，J，K)LDPC码，N表示码长，J和K分别表示校验矩阵H行和列的重量。LDPC码可以用Tanner图表示。Tanner图由变量节点、校验节点以及连接变量节点和校验节点的边组成。变量节点c_i对应矩阵H中的第i列，校验节点v_j对应矩阵H中的第j行。如果h_ij=1，表明Tanner图中节点v_j和c_i由一条边相连，否则不相连。图1所示为规则(6，2，3)LDPC码的Tanner图，校验节点和变量节点分别用方框和圆表示。每个节点连接的边的个数称之为该节点的度，图1所示LDPC码的校验节点和变量节点的度分别为3和2^[13]。

其中，n_i是服从均值为0、方差为δ²的高斯白噪声(表示为n_i～N(0，δ²))，且它们之间相互独立。E_b/N_o表示信噪比(Signal-to-Noise Ratio，SNR)，E_b表示发送前每个信息比特的能量，N_o表示发送前噪声功率谱密度以及δ²=N_o/2。在开始进行译码前，对于通过一个BPSK AWGN信道的码字，最终接收序列的每个码字的先验概率的对数似然比(LLR)初始化为：

    式(3)和式(4)描述了译码过程中LDPC码变量节点和校验节点之间的消息更新和传递规律。RBP和NWRBP算法是将剩余度值作为度量去调整更新顺序的两种主要算法机制。剩余度是消息更新之前和之后差值的绝对值。在LDPC译码中，剩余度值的定义值为：  

    作为RBP的扩展和延伸，RBP算法和NWRBP算法两者的区别是：RBP动态选择最大剩余度所在的边进行更新，而NWRBP动态选择最大剩余度所在的校验节点进行更新。NWRBP详细步骤见算法1。

    算法1：LDPC码的NWRBP算法译码流程

2 ENWRBP算法机制描述

    由于RBP译码算法和NWRBP译码算法每次通过一条边或是一个校验节点去更新传播消息，这样会形成一个个相对独立彼此没有影响的子集合，经过数次迭代后，可能就会导致忽略掉已经被正确修改的错误比特节点，再一次出现错误，所以，RBP算法和NWRBP算法都具有一定的贪婪性。而NWRBP译码算法根据节点更新消息，每个子集合范围较大，其贪婪性相对较弱。因此，经过大量的迭代译码后，NWRBP算法的译码性能会优于RBP算法译码性能。然而，这两种算法的性能受限于陷井集(trapping sets)的影响，导致一些错误的变量节点(即误码)在迭代多次后很难被发现。经研究发现，NWRBP在译码过程中，节点更新的次数并不均衡，存在某些节点更新次数少的现象，而相对于更新次数较多的变量节点，更新次数较少的变量节点不能为相邻节点提供足够的有用信息，亦或该节点无法从相邻节点获得有用信息，导致相邻节点或其本身发生错误的概率更大。本文正是利用此思想来减少带来的误差，在NWRBP译码算法的基础上提出一种改进算法Enhanced NWRBP(ENWRBP)。在NWRBP译码算法的一次译码过程中，如果达到最大的迭代次数仍然不满足译码成功条件，那么就寻找到在迭代过程中更新最少次数的变量节点v_min，并且将最初经高斯白噪声信道接收到的序列对应的初始对数似然数r_min设置为0。随后，重新用NWRBP进行译码，直到译码成功或连续重复T上述过程，即更新T次最少的变量节点。ENWRBP算法过程描述如图2，详细步骤见算法2。

    算法2：LDPC码的ENWRBP算法译码流程

3 仿真结果与讨论

    本文中所有的仿真都是在二进制输入加性高斯白噪声(BI-AWGN)信道进行的。译码方式采用基于剩余度置信传播(RBP)算法、基于校验节点的剩余度置信传播(NWRBP)算法,以及本文提出的基于校验节点的改进剩余度置信传播(ENERBP)算法，最大迭代次数设为100，调制方式为BPSK，具体的仿真结果如图3~图6所示。

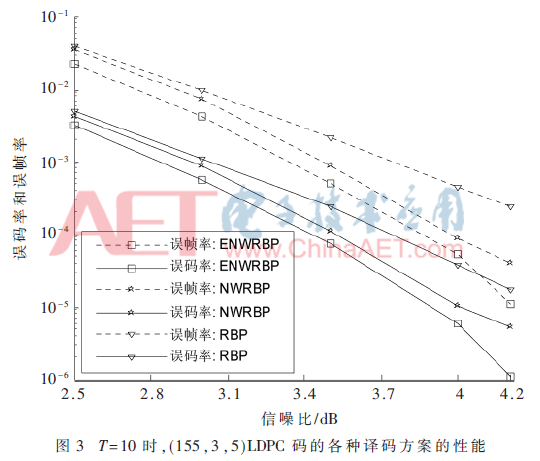
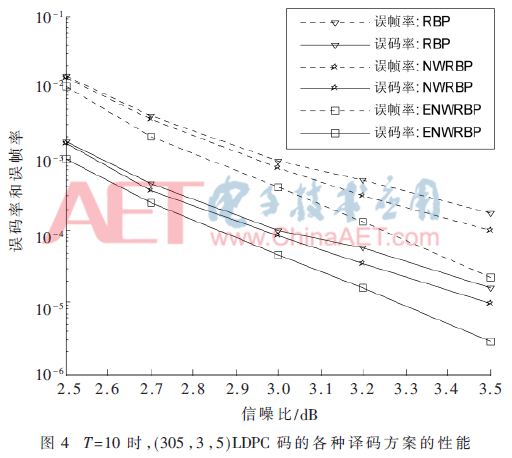
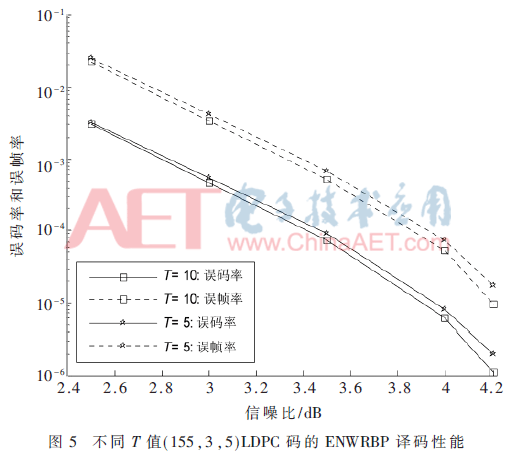
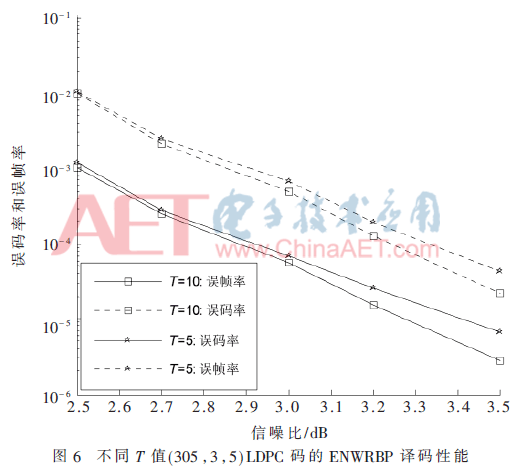
    图3和图4中T=10时，可以观察到ENWRBP算法的译码性能要好于NWRBP和RBP算法。在SNR值较低时，图3中SNR值为2.5～3 dB，图4中为2.5～2.7 dB，误码率BER和误帧率FER的曲线三者大致相同。随着SNR值的增加，ENWRBP算法和NWRBP算法的译码曲线逐渐优于RBP算法，图3中NWRBP算法和ENWRBP算法依然大致相同，直到SNR值为4.0 dB时，ENWRBP算法开始优于NWRBP算法，图4中ENWRBP算法在所示SNR范围内始终优于RBP算法和NWRBP算法，并且这种优势随着SNR值增大而逐渐扩大。例如：如图4所示，在FER=2×10^-4时，相比RBP和NWRBP，ENWRBP的FER分别得到0.3 dB和0.18 dB的译码增益；同样，在BER=2×10^-5时，相比RBP和NWRBP，ENWRBP的BER分别得到0.28 dB和0.16 dB的译码增益。

    通过图5和图6 ENWRBP译码性能的比较，可以观察到，T=10时的曲线要低于T=5时的曲线，并且这种趋势随着SNR值的增大而增大。例如：如图6所示，在FER=1×10^-4时，相比T=5，T=10得到0.8 dB的译码增益；同样，在BER=1×10^-5时，相比T=5，T=10得到1.2 dB的译码增益。由此可见，通过增大变量节点初始LLR值置0尝试次数，可进一步提高ENWRBP译码性能。

4 结论

    本文在NWRBP算法的基础上介绍了一种增强译码算法ENWRBP(Enhanced NWRBP)。相比较NWRBP算法，该算法的译码性能优于NWRBP，特别是SNR值稍大时尤为明显。仿真表明，NWRBP在每次迭代过程中，更新次数少的变量节点，其本身或相邻节点发生误码的概率高于其他的变量节点。ENWRBP译码算法针对这一点，多次找到更新次数最少的变量节点，然后对该节点的初始化值置0，并重新译码，从而提高了NWRBP算法译码性能。另外，本文提出的基于节点更新次数最小、置零初始化值的思路也可以运用于其他LDPC译码算法中。

参考文献

[1] Li Hua，Zheng Linhua.Efficient puncturing scheme for irregular LDPC codes based on serial schedules[J].IEEE Communications Letters，2015，19(9)：1508-1511.

[2] 白宝明，孙成，陈佩瑶，等.信道编码技术新进展[J].无线电通信技术，2016，42(6)：1-8.

[3] MACKAY D J C，NEAL R.Near Shannon limit performance of low density parity check codes[J].IEEE Electronics Letters，1998，33(6)：457-458.

[4] 郑伟，马晓越，赵成晨.一种改进的LDPC码BP译码算法[J].河北大学学报(自然科学版)，2016，36(5)：547-553.

[5] 张福星，许生旺.一种改进的多元LDPC码译码算法[J].无线通讯技术，2016，42(6)：56-81.

[6] GOLOV O，AMRANI O.Edge-based scheduled BP in LDPC codes[C].IEEE International Symposium on Information Theory，2007：2376-2380.

[7] SAEJOON K，KARAM K.Two-staged informed dynamic scheduling for sequential belief propagation decoding of LDPC codes[J].IEEE Communication Letters，2009，13(3)：193-195.

[8] LEE H C，UENG Y L，YEH S M，et al.Two informed dynamic scheduling strategies for iterative LDPC decoders[J].IEEE Transactions on Communications，2013，61(3)：886-896.

[9] CASADO A I V，GRIOT M，WESEL R D.LDPC decoders with informed dynamic scheduling[J].IEEE Transactions on Communications，2010，58(12)：3470-3479.

[10] Song Lingyan，Hou Shujuan.Improved decoding of LDPC codes by variable-to-check residual belief propagation[C].International Conference on Communications & Networking in China，2015：163-166.

[11] Liu Xingcheng，Zhang Yuanbin，Cui Ru.Variable-node-based dynamic scheduling strategy for belief-propagation decoding of LDPC codes[J].IEEE Communications Letters，2015，19(2)：147-150.

[12] Han Guojun，Liu Xingcheng.An efficient dynamic schedule for layered belief-propagation decoding of LDPC codes[J].IEEE Communications Letters，2009，13(13)：193-195.

[13] KSCHISCHANG F R，FREY B J，LOELIGER H A.Factor graphs and the sum-product algorithm[J].IEEE Transactions on Information Theory，2001，47(2)：498-519.

作者信息：

周  华1，2，3，翁少辉1，3，冯  姣1，3

(1.南京信息工程大学，江苏 南京210044；2.江苏省大气环境与装备技术协同创新中心，江苏 南京210044；

3.江苏省气象探测与信息处理重点实验室，江苏 南京210044)