广义主分量分析及其在人脸识别中的应用
2008-05-06
作者:郭 娟1,戚文芽1,岳 峰2
摘 要: 传统的主分量分析在处理图像识别问题时是基于向量的。结合视频监控应用的特点,实现了两种直接基于图像矩阵的广义主分量分析方法。经使用ORL人脸" title="人脸">人脸库试验比较,该方法不仅在识别性能上优于经典的Eigenfaces和Fisherfaces方法,且大大加快了特征抽取的速度,满足了视频监控系统" title="视频监控系统">视频监控系统中人脸识别" title="人脸识别">人脸识别实时性的需求。
关键词: 广义主分量分析 主分量分析 特征抽取 人脸识别
近年来,数字视频监控在各行各业得到了广泛应用,如军事上、小区和楼宇安全监控、银行证券系统、林业部门火情监控、交通违章和流量监控等。视频监控系统对被监控目标的自动识别,给监控部门提供了更多的信息保障,降低了犯罪率,并节省了人力和物力。人脸识别技术就是通过计算机分析人脸图像,从中提取有效的识别信息,从而辨认身份的一种技术。它是一种非侵犯式的主动识别,易为广大人群所接受。人脸识别不仅在视频监控方面,在其他诸如安全验证系统、信用卡验证、视频会议、人机交互等方面都具有十分广阔的应用前景。
人脸识别的方法很多,主分量分析PCA(也称K-L变换)是特征抽取最为经典的方法之一,目前仍被广泛地应用在人脸等图像识别领域[1][2]。尽管PCA方法的性能不错,但是传统做法的缺点明显:首先,将图像矩阵转化为图像向量,然后以该图像向量作为原始特征进行PCA。由于图像向量的维数一般较高,给随后的特征抽取造成了困难。若图像的分辨率为100×100,则所得图像向量的维数高达10 000,在如此高维的图像向量上完成PCA是非常耗时的。尽管利用奇异值分解定理可加速总体散布矩阵特征向量" title="特征向量">特征向量的求解速度,但整个特征抽取过程的计算量仍相当可观。
考虑到视频监控系统的实时性需求,本文借鉴Liu[3]代数特征抽取的新思路,直接利用图像矩阵构造图像散布矩阵,实现了基于两种图像矩阵的广义主分量分析方法。该方法简单易行,不仅在识别性能上优于Eigenfaces[4]和Fisherfaces[5]方法,其突出特点是特征抽取的速度大大加快,从根本上克服了传统PCA耗时过多的弱点,满足了视频监控系统中自动人脸识别实时性的需求。
1 经典的主分量分析
PCA技术最早由Sirovich和Kirby引入人脸识别领域,其主要思想是降维,以Turk和Pentland的Eigenfaces方法最具代表性[6],该方法的具体过程如下:
设人脸灰度图像的分辨率为m×n,则该图像构成一个m×n的图像矩阵A。首先将图像矩阵A转化为N=m×n维的图像向量x,根据训练样本集构造N×N的总体散布矩阵St:
St=E(x-Ex)(x-Ex)T (1)
选取一组标准正交且使得准则函数式(2)达到极值的向量ξ1,…,ξd,做为投影轴,其物理意义是使投影后所得特征的总体散布量(类间散布量与类内散布量之和)最大" title="最大">最大。
Jt(ξ)=ξTStξ (ξTξ=1) (2)
由于准则函数式(2)等价于

式(3)即为矩阵St的Rayleigh商。由Rayleigh商的极值性质[7],最优投影轴ξ1,…,ξd可取为St的d个最大特征值所对应的标准正交的特征向量。
2 广义主分量分析
2.1 基于图像总体散布矩阵的主分量分析
设X表示n维列向量,基于图像矩阵的PCA就是将m×n的图像矩阵A通过线性变换Y=AX直接投影到X上,得到一个m维列向量Y,称为图像A的投影特征向量。
决定最优投影轴X最直观的办法是通过投影特征向量Y的散布情况来决定投影方向X。通常采用以下准则:
Jt(X)=tr(MTx) (4)
其中,MTx表示投影特征Y的总体散布矩阵,tr表示取矩阵的迹。最大化准则(4)式的直观意义是:寻找这样的投影方向X,使投影后所得特征向量的总体散布量最大。
称(9)式为广义总体散布量准则。最大化该准则的单位向量X称为最优投影轴,其物理意义是,图像矩阵在X轴上投影后所得的特征向量的总体分散程度最大。事实上,最优投影轴即为图像总体散布矩阵Mt的最大特征值所对应的单位特征向量。
在样本类别数较多的情况下,单一的最优投影方向是不够的,需要寻找一组满足标准正交条件且最大化准则函数(9)式的最优投影轴X1,…,Xd。因此,准则函数(9)式等价于:
2.2 基于图像类间散布矩阵的主分量分析
上节的分析中,采用的是广义总体散布量准则,考虑到以样本的可分性最好为目标,还可以在(4)式中采用另一准则:
Jb(X)=tr(MBx) (11)
其中,MBx表示投影特征向量Y的类间散布矩阵,其物理意义是,图像矩阵在X方向上投影后所得特征向量的类间分散程度最大。
同前面的分析,首先给出MBx的估计:
相应地,最优投影轴为矩阵Mb的最大特征值所对应的单位特征向量。同样,考虑到需要抽取多个投影轴,准则函数(14)式等价于下式:

最优投影轴X1,…,Xd即可取为Mb的d个最大特征值所对应的标准正交的特征向量。
2.3 特征抽取
设最优图像投影轴为X1,…,Xd,由
Yk=AXk,k=1,2,…,d (17)
得到一组投影特征向量Y1,…,Yd,称为图像A的主成分,可将其合并为一个m×d维的图像A的整体投影特征向量B用于后面的分类识别。
B=[Y1,…,Yd]T=A[X1,…,Xd]T=AP (18)
其中,P=[X1,…,Xd]T。
2.4 分类
3 试验与分析
ORL人脸库由40人、每人10幅112×92的图像组成,其中有些图像拍摄于不同的时期;人脸表情与脸部细节有着不同程度的变化,如笑或不笑、眼睛睁或闭、戴或不戴眼镜;人脸姿态也有相当程度的变化,深度旋转与平面旋转可达20°;人脸的尺度也有多达10%的变化。图1是ORL人脸库中某一人的5幅图像。

本试验中,以每人的前5幅图像作为训练样本,后5幅作为测试样本,这样训练样本和测试样本的总数均为200,属于典型的高维小样本识别问题。分别构造图像总体散布矩阵Mt和图像类间散布矩阵Mb,并分别计算其前10个最大特征值所对应的标准正交特征向量X1,…,X10,选取其中的1到10作为投影轴进行(18)式的特征抽取。在此,人脸灰度图像是112×92矩阵,若取k个投影轴,则所得整体投影特征向量的维数是112×k。
试验1:在每个投影空间内,对两种基于图像矩阵(图像总体散布矩阵Mt和图像类间散布矩阵Mb)的主分量分析分别采用最小距离分类器和最近邻分类器进行分类,识别率见表1。

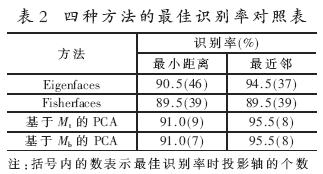
试验2:比较了本文两种基于图像矩阵的主分量分析方法与经典的Eigenfaces、Fisherfaces方法在最近邻分类器下的识别率,结果见表2。
试验3:比较了上面四种方法在取得最佳识别率时的特征抽取和识别时间,结果见表3。
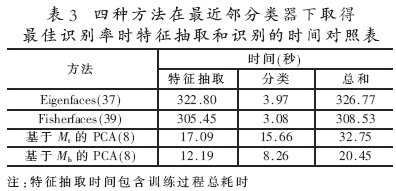
由表1、表2可见,两种基于图像矩阵的主分量分析方法在两类分类器下的识别率相差不大,其性能都优于Eigenfaces和Fisherfaces方法。由表3可见,在时间方面,基于图像类间散布矩阵Mb的主分量分析的特征抽取速度最快,是Eigenfaces、Fisherfaces方法的近26倍。这是因为在基于Mb的主分量分析中,Mb是92阶的,而在Eigenfaces和Fisherfaces方法中需处理112×92=10 304阶的总体散布矩阵,尽管利用奇异值定理可加速总体散布矩阵的特征向量的求解速度,但计算量仍很大,因此耗时过多。
本文结合视频监控系统中人脸识别实时性的需求,实现了两种基于图像矩阵的广义主分量分析的人脸识别方法。与传统主分量分析处理图像识别问题不同,该方法不需要事先将图像矩阵转化为图像向量,而是直接利用图像矩阵本身构造形如(8)式和(15)式所示的图像散布矩阵,然后取它的d个最大特征值所对应的标准正交的特征向量作为投影轴即可。实验结果表明,该方法不仅在识别性能上优于经典的Eigenfaces和Fisherfaces方法,最突出的优点是大幅度地降低了计算量,使特征抽取的速度提高了一个数量级,且方法简单易行,适于实时视频监控系统的应用。
参考文献
1 Pentland A.Looking at people:Sensing for ubiquitous and wearable computing[J].IEEE Transactions on Pattern Analysis And Machine Intelligence,2000;22(1):107~109
2 Grudin M A.On internal representations in face recognition systems[J].Pattern Recognition,2000;33(7):1161~1177
3 Liu K,Cheng Y Q,Yang J Y.Algebraic feature extraction for image recognition based on an optimal discriminant criterion[J].Pattern Recognition,1993;26(6):903~911
4 Turk M,Pentland A.Face recognition using eigenfaces[A].In: Proceedings IEEE conference on computer vision and pattern recognition[C],Hawaii,1991:586~591
5 Belhumeur P N,Hespanha J P,Kriengmam D J.Eigenfaces vs.Fisherfaces:Recognition using class specific linear projec-tion[J].IEEE Transactions on Pattern Analysis And Machine Intelligence,1997;19(7):711~720
6 周 杰,卢春雨,张长水等.人脸自动识别方法综述[J].电子学报,2000;28(4):102~105
7 程云鹏.矩阵论[M].西安:西北工业大学出版社,1999:294~302

