MIMO系统中优化功率分配算法的研究
2008-07-14
作者：杜丽霞
摘 要: MIMO技术作为未来移动通信" title="移动通信">移动通信中关键技术，其系统的功率分配" title="功率分配">功率分配问题在未来移动通信发展中非常重要。在传统WF(Water-Filling)功率分配算法基础上提出了一种优化自适应功率分配算法QOSWF，并对该算法的有效性进行了MATLAB仿真研究。
关键词: MIMO 功率分配 QOSWF MATLAB
在MIMO系统中应用WF算法可以在理论上获得最优的容量增益，但是这种算法假设量化度为无限小，因此并不可行。而在传统的比特分配算法中，等功率自适应比特分配算法虽然计算量小，算法复杂度低，但功率等分会造成资源浪费以及系统性能" title="系统性能">系统性能下降较大， Hughes-Hartongs算法和Fisher算法虽然可以非常有效地优化系统性能，但受 “恒定间隔”的限制，且计算量也随着承载的比特数和子信道数目的增大而迅速提高，不适合应用在空间子信道相对较少的MIMO系统中。为了克服WF算法和传统的比特分配算法的这些不足，本文给出了一种可以有效利用频率资源来提高系统性能，且更符合实际情况的自适应比特功率分配算法。
1 优化算法介绍
基于QOS的WF算法是WF算法与比特分配算法两者的结合。该算法的优化目标为在满足给定的误比特率" title="误比特率">误比特率条件下，最大化各子信道的比特传输速率。它首先以WF算法为基础根据各个子信道的衰落特性进行初始的比特和功率分配，再求出在满足所要求的QOS的情况下，各个子信道所应该分配的最小功率及比特数，也就是调制阶数；然后对剩余的功率和比特进行再分配。再分配是按照下文所示的步骤来进行的，主要通过信噪比" title="信噪比">信噪比和调制阶数的交互计算来完成，分配直至达到总功率的限制为止。这里的QOS指的是所限制的误比特率的门限值。
该算法过程可以描述如下：假设Mi，ρi和βi分别表示第i个正交子信道的调制阶数、信噪比和误码率，则有:
其中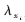
为各信道所分配的功率，λH,i为H矩阵的奇异值，σ2为基带噪声功率。对于给定的调制方式，根据文献很容易得到在AWGN信道下误码率和信噪比的关系。为了更直观地说明，图1给出了仿真得到的AWGN信道下各种调制制式的BER曲线。
这里以BER为10-3为例，根据图1可以得到Mi等于2～256进制的各种调制制式下满足此QOS的信噪比门限，为了以后计算方便，把各种调制制式关系下的这个门限值用图表表示出来，如表1所示。
根据(1)式，可以得到各个子信道的信噪比ρi，根据表1就可以确定各个子信道可以承载的调制方式，并找出所确定的调制方式下相对应的SNR门限，再用各个子信道的ρi分别减去这些相应的SNR门限，即可得到剩余的功率。为了方便，这里用函数F来表示调用这个表的作用。
则上述过程可以表示如下:
这里设信噪比门限为Γi，则有:
这里Φ表示所设定的目标误比特率。这个基于QOS的WF算法的优化目标是在保持目标误比特率不变的情况下，使各个子信道的比特速率最大化。可以用以下两个子式来表示:
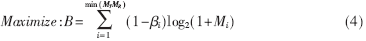
且满足:
在一定的QOS限制下，如果确定信道调制阶数，会有一个信噪比门限来满足这个要求，若不能达到更高的调制阶数，则给各个子信道多分配在信噪比门限之上的功率是完全没有必要的，因为这样并不会增加信道的比特传输速率。基于QOS的WF算法的主要思想就是有效地利用最少的功率资源来满足QOS的要求，来获得一些剩余的功率，对这些剩余的功率进行再分配，以尽可能地提高各子信道的比特速率。对于剩余的功率，可以用一个带有参数的流程来进行再分配，这个流程可以表示如下:
计算现在剩余的功率:
找到在QOS限制下的各子信道最大可能的Mi：
找到可以满足Mi的信噪比门限:
计算各子信道所对应的需要的发射功率:
基于QOS的WF算法在满足误比特率的前提下，尽可能地把剩余的功率按顺序分配到各个子信道，获得更高的调制阶数。如果可以获得更高的调制阶数，则重新分配剩余功率，直至分配完毕。
这个算法具体步骤可以表示如下:
(1)计算基于WF算法的
(2)v=0，从1到min(MT,MR)运行上面给出的再分配流程;
(3)v=1，从1到min(MT,MR)运行上面给出的再分配流程;
(4)对所有子信道进行功率再分配，直至总功率分配完毕。
基于QOS的WF算法在满足误比特率的前提下，对BER和调制阶数的关系进行交替使用，各子信道的比特速率在QOS的限制下，有一定的提高。此算法的复杂度与WF算法相近，因为各个子信道所分配的最初功率值是由WF算法得到的。将对此算法和简单量化后的WF算法进行仿真分析比较。仿真时遇到有的子信道的信噪比非常低，以致连二阶调制的误比特率门限值都达不到，对于这种情况，为了保证整个系统有一个固定的QOS水平，在这里对这些性能较差的子信道实行关闭，也就是说不用它们发射信号，以此来保证整个系统能维持一定的服务质量水平。
2 算法的仿真分析
首先简要介绍经常使用的自适应速率量化和功率分配的算法SR(Simple Rate)简单速率量化算法。SR速率量化算法只是简单地对分配的总发送功率按“注水”原理进行分配，然后进行量化，折算出离散速率。这种算法虽然计算量小，但是由于它仅仅是对所分配的功率进行了简单的量化，所以肯定会存在一些剩余的功率未被使用，从而造成资源的浪费。
(1)先根据 WF算法，求得最初的
(2)在QOS的限制下，找到最大可能的Mi值
仿真时不考虑信道编码，传输的中断概率(Poutage)为0.01， QOS要求BER必须低于门限值10-3，σ2=1。MIMO系统结构分别为2×2,4×4。
同时对QOSWF算法下的误码率也进行仿真，根据MIMO道下的误码率，可以通过对各个子信道的误码率求均值得到。这里假设MIMO系统在调制阶数为2和4时，采用MPSK的调制方式，在调制阶数大于4时，采用MQAM调制方式。
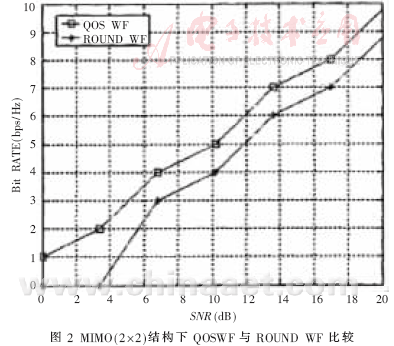
从图2和图3可以看到，QOS WF算法通过上面所讲述的方法对所剩余的功率进行再分配后，它的比特速率比简单的ROUND WF算法有很明显的提高。其中，在2×2的天线结构中，所提高的比特速率平均约有1bps/Hz，而对于4×4的天线结构，比特速率约有2～4bps/Hz的提高。
参考文献
[1] 张平, 王卫东, 陶小峰.WCDMA移动通信系统. 北京：人民邮电出版社，2001.
[2] 郭梯云, 邹国扬, 李建东.移动通信.西安：西安电子科技大学出版社，1995.
[3] 王松桂, 程维虎, 高旅端.概率论与数理统计. 北京：科学出版社，2000.
[4] 杨大成.移动传播环境:理论基础、分析方法和建模技术.北京：机械工业出版社,2003.
[5] 张涛. 基于MIMO信道的高速数据的传输研究[D].西安:西安电子科技大学，2005.
[6] DHAHIR N A. FIR channel-shortening equalizers for MIMO ISI channels, IEEE Traps. Commun.，2001,49:213-218.