0 引言

    煤气鼓风机能否正常运行关系到冶金、化工等行业是否能顺利生产，在煤炭、钢铁等行业中占有十分重要的地位^[1-2]。关于鼓风机故障模式识别的方法有很多，如神经网络方法、振动信号处理方法等多种方法^[3]。其故障频谱具有周期性及随机噪声大的特点，针对这一特点，本文拟采用一种新的频谱估计方法，该方法建立在传统的频谱估计法基础上改进而成。

    频谱分析分为连续谱分析与离散频谱分析，两种分析方法在许多领域得到了广泛应用，后者是本文研究的重点。离散频谱分析法实现了信号处理从时域到频域的转变，在电子、机械、雷达测速及激光多普勒测速技术等众多领域得到了大力推广。如KIM H H于2008年运用DFT算法对电弧进行故障检测^[4-7]。然而这些方法都存在一些缺点，尤其在频谱泄露的问题仍然没得到很好的解决，这将导致计算出的信号、频率、相位发生较大误差。尤其在机械故障信号频谱存在大量随机噪声时，其估计精度均很低^[8-10]。因此，本文提出一种新的DFT插值算法来判断煤气鼓风机等旋转机械的故障频谱，从而为分辨出具体的故障类型提供良好的促进作用。通过数值计算和计算机仿真，证实了该方法的有效性，并将其与传统的比值校正法进行了比较研究。

1 理论背景

    为了推导离散频谱估计的理论算法，设伴有高斯白噪声的单一频率的正弦信号的表达式为：

式中，f_s和N分别代表采样频率和采样点数，则相应的频率分辨率为Δf=f_s/N，且采样频率f_s须满足f_s≥2f₀才能满足采样定理。若在非同步采样条件下得到的采样信号，则归一化频率将位于最大谱线与第二大谱线之间，故可表示成下式：

其中，Ψ₀表示归一化频率，β_w与μ_w分别代表归一化频率的整数部分与小数部分。若使信噪比(SNR)大于某个设定阈值，则β_w的值可通过窗谱峰值搜寻算法确定。小数部分μ_w也称频率偏差，其值可通过加窗与离散傅里叶变换求得。

2 提出的插值DFT算法

2.1 算法描述

    本节主要运用加零技术与插值算法的优点，提出一种新方法，该方法能较快确定频谱的整数部分与小数部分，从而达到频谱校正的目的。

    设采用加零法的离散信号样本的表达式为：

2.2 其他经典窗函数的扩展

    本节将重点介绍采用主瓣拟合算法的其他经典窗函数的扩展。定义函数X(k)为：

式中，W(·)是窗函数的离散时间傅里叶变换，已有研究表明，若k值在（0.5，0.5]区间内，很多经典窗函数的|S(k)|的值非常小。如Blackman窗的|S(k)|值不超过10^-4，Hamming窗的值不超过10^-5，即[W_O(k)]^p与W_H(k)在它们主瓣中心可相互匹配。故只需将k值限制在[-0.5，0.5]之内，则上述插值算法可以扩展到其他经典窗函数。在实际应用中采用加零法时，考虑到计算量及基-2FFT算法，常取值λ=4。

3 应用实例

    为了更真实地评价新算法对频率偏差估计方面的能力，用MATLAB和VC6.0编程实现上述新算法。将归一化频率偏差μ设定在（-0.5，0.5）之间，扫描步长为0.05 Hz，采样频率f_s为1 024 Hz，采样点数N也设定1 024。下面以煤气鼓风机为实例对新算法有效性进行验证分析。先采用数个加速度传感器和速度传感器对煤气鼓风机的振动信号进行实测。

    经过一段时间后获得的由加速度传感器测得的煤气鼓风机3#轴瓦故障频谱实例如图1所示。

    将该故障时域波形经新算法估计后得到其频域图形，如图2所示。图2中故障特征频率为184.5 Hz，刚好为鼓风机转速频率的3倍（f=61.5 Hz）,而轴不对中的故障频率恰好为185 Hz，经分析，初步认为该煤气鼓风机发生了轴系不对中的故障。随后安排工作人员拆开该煤气鼓风机，经现场仔细检查发现确实是3#轴与2#轴系不对中，经过校正将轴系对正，该不对中故障现象消失了。故可以认为新算法在机械故障谱估计方面具有较高精度。

4 比较研究

    在频率校正中，在噪声条件下的估计精度是衡量算法优越性的一个重要指标。当有噪声存在且较高时，即便将信噪比设得过高，使其远大于阈值时，使用上述传统算法对频率校正时仍可能将正确谱线估计在错误位置，这种情况在频谱校正中通常被称为不正确的极性估计（简称IPE）。当发生IPE现象时，将不仅严重影响信号反转的结果，而且会极大影响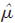的值。

    机械设备故障信号中往往包含大量噪声，为了检验新算法在抗加性噪声方面的性能，本节将新算法与传统算法作了比较分析。在比较研究之前，先假设有一个被伴有加性噪声的理论信号，信噪比设为-5 dB，使之发生不正确的极性估计(即IPE现象)。设定步长为0.025 Hz，扫描频率区间从255.5 Hz～256.5 Hz，且随机相位均匀分布于[-π，π]间。对于每个频率均产生50 000个独立的实例。

    图3显示了新算法与传统算法在汉宁窗时频率偏差函数的标准差误差及平均绝对误差。

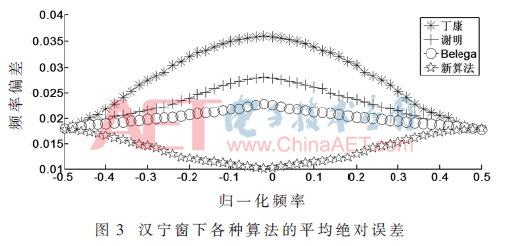
    由图3可知，传统的3种算法中在加性噪声条件下的估计精度均很高，随着|μ|增大，这3种算法的频率校正误差（包括标准差误差与平均绝对误差）均增大。当μ值处于(-0.5，0.5)范围中，丁康算法在噪声条件下的估计误差在所有算法中最大，其误差曲线先上升到一个最高点，然后继续下降并达到一个较高水平。然而，本文提出的新算法在μ值处在(-0.5，0.5)范围时其估计误差除了少数几个波动之外几乎均相等,且其估计误差值在所有算法的估计结果中是最小的。图4与图5还显示了海明窗和Blackman窗的估计误差的标准差。可以看出，包括新算法在内的各算法的结果与图3的汉宁窗时仿真结果基本相同。

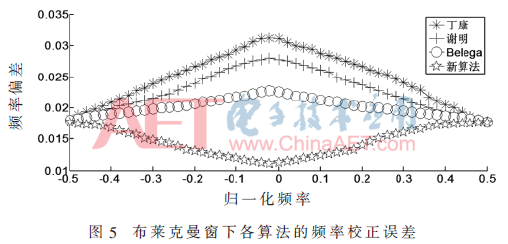
    综上所述，各算法的仿真研究表明，传统算法在噪声条件下的估计误差均较低，而新算法的估计误差的标准差在所有算法中最低，从而显示出其较强的抗IPE性能。

5 结论

    针对鼓风机故障频谱具有周期性及伴随噪声的特点，在补零技术与主瓣拟合技术的基础上，本文提出了一种新的基于插值DFT的频率校正方法。该方法具有简便快捷且实用性强的特点，能与许多其他经典的窗函数相兼容，而且它不需要知道数据窗函数的频谱，或进行任何的先验计算。其缺点就是增加了FFT的计算量。通过计算机仿真分析，针对各种窗函数将新算法有效性与传统算法进行了比较分析与验证。通过应用实例分析，表明新算法可应用于煤气鼓风机故障频谱，甚至旋转机械故障频谱的准确校正。比较分析与仿真结果表明，新算法在有噪声时估计误差更低，且其具有对IPE更强的稳健性。

参考文献

[1] 张亢，程军圣，杨宇.基于局部均值分解与形态谱的旋转机械故障诊断方法[J].振动与冲击，2013，32(9)：135-139.

[2] 王凤利，马孝江.局域波分形动力学在旋转机械故障诊断中的应用[J].农业机械学报，2004，35(2)：134-137.

[3] 顾伟，黄志毅，章卫国，等.飞控系统神经网络故障模式分类方法研究[J].计算机仿真，2011，28(5)：52-55.

[4] KIM H H，LEE C J，PARK J B，et al.Two-terminal numerical algorithm for single-phase arcing fault detection and fault location estimation based on the spectral information[J].Journal of Electrical Engineering & Technology，2008，3(4)：460-467.

[5] BURGESS J C.On digital spectrum analysis of eriodic signals[J].J.Acoust.Soc.Am，1975，58(3)：556-567.

[6] XIE M，DING K.Correction for the frequency,amplitude and phase in FFT of harmonic sigial[J].Mechanical System and Signal Processing，1996，10(2)：211-221.

[7] 丁康，陈健林，苏向荣.平稳和非平稳振动信号的若干处理方法及发展[J].振动工程学报，2003，16（1）：1-10.

[8] SANTAMRIA I，PANTALEON C，IBANEZ J.A comparative study of high-accuracy frequency estimation methods[J].Mechanical System and Signal Processing，2000，14(5)：819-834.

[9] DUDA K.DFT interpolation algorithm for Kaiser-Bessel and Dolph-Chebyshev windows, instrumentation and measurement[J].IEEE Transactions on Istrumentation & Measurement，2011，60(3)：784-790.

[10] 丁康，张晓飞.频谱校正理论的发展[J].振动工程学报，2000，13（1）：14-22.

作者信息：

谢长贵1，2，陈  平2

(1.重庆工程职业技术学院 机械工程学院，重庆402260；2.重庆大学 机械工程学院，重庆400044)